题目内容
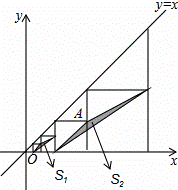
如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数y=x的图象上,从左向右第3个正方形中的一个顶点A的坐标为(8,4),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn,则Sn的值为 .
24n-5
【解析】
试题分析:根据直线解析式判断出直线与x轴的夹角为45°,从而得到直线与正方形的边围成的三角形是等腰直角三角形,再根据点A的坐标求出正方形的边长并得到变化规律表示出第n个正方形的边长,然后根据阴影部分的面积等于一个等腰直角三角形的面积加上梯形的面积再减去一个直角三角形的面积列式求解并根据结果的规律解答即可.
解:∵函数y=x与x轴的夹角为45°,
∴直线y=x与正方形的边围成的三角形是等腰直角三角形,
∵A(8,4),
∴第四个正方形的边长为8,
第三个正方形的边长为4,
第二个正方形的边长为2 ,
,
第一个正方形的边长为1,
…,
第n个正方形的边长为2n-1,
由图可知,S1=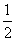 ×1×1+
×1×1+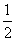 ×(1+2)×2-
×(1+2)×2-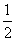 ×(1+2)×2=
×(1+2)×2=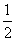 ,
,
S2=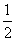 ×4×4+
×4×4+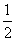 ×(2+4)×4-
×(2+4)×4-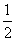 ×(2+4)×4=8,
×(2+4)×4=8,
…,
Sn为第2n与第2n-1个正方形中的阴影部分,
第2n个正方形的边长为22n-1,第2n-1个正方形的边长为22n-2,
Sn=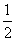 •22n-2•22n-2=24n-5.
•22n-2•22n-2=24n-5.
【难度】较难

 小学期末标准试卷系列答案
小学期末标准试卷系列答案为了从甲、乙两名选手中选拔一个参加射击比赛,现对他们进行一次测验,两个人在相同条件下各射靶10次,为了比较两人的成绩,制作了统计表和统计图:
甲、乙射击成绩统计表
| 平均数 | 中位数 | 方差 | 命中10环的次数 | |
| 甲 | 7 | 0 | ||
| 乙 | 1 |


(1)请补全上述图表(直接在表中填空和补全折线图);
(2)如果规定成绩较稳定者胜出,你认为谁应胜出?说明你的理由;
(3)如果希望(2)中的另一名选手胜出,根据图表中的信息,应该制定怎样的评判规则?为什么?
 的值为 .
的值为 .

 上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .
上的点,A、B两点的横坐标分别是a、2a,线段AB的延长线交x轴于点C,若S△AOC=6,则k的值为 .

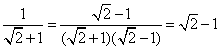 ;
;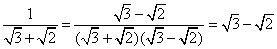 ;
;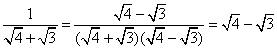 ;
; ;
;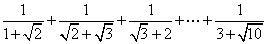 .
.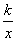 (x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=
(x>0)的图象经过点A(2,a)(a>0),过点A作AB⊥x轴,垂足为点B,将线段AB沿x轴正方向平移,与反比例函数y=