题目内容
10.(1)如图①,已知D、E分别是△ABC的边AB、AC上一点,DE∥BC,连接CD、BE,CD、BE交于点F,连接AF并延长,分别交DE、BC于点H、G.求证:①$\frac{DH}{BG}=\frac{HE}{GC}$;
②G是BC的中点.
(2)运用(1)中的方法,在图②中,只用一把无刻度的直尺画出矩形ABCD的一条对称轴.(不写画法,保留画图痕迹)

分析 (1)①由DE∥BC,得到△ADH∽△ABG和△AHE∽△AGC,即可得到结论;
②易证△DEN∽△AEM,△OND∽△OMB,则依据相似三角形的对应边的比相等,可以证得$\frac{GC}{BG}=\frac{BG}{GC}$,得到BG=CG即可;
(2)①连接AC,BD,两线交于点O1.②在矩形ABCD外任取一点E,连接EA,EB,分别交DC于点G,H③连接BG,AH,两线交于点O2.④作直线EO2,交AB于点M.⑤作直线MO1.直线MO1就是矩形ABCD的一条对称轴.
解答 (1)证明:①∵DE∥BC,
∴△ADH∽△ABG,
∴$\frac{DH}{BG}=\frac{AH}{AG}$,
同理:$\frac{HE}{GC}=\frac{AH}{AG}$,
∴$\frac{DH}{BG}=\frac{HE}{GC}$;
②∵DE∥BC
∴△FDH∽△FCG,
∴$\frac{DH}{GC}$=$\frac{FH}{FG}$,
同理:$\frac{EH}{GB}=\frac{FH}{FG}$,
∴$\frac{DH}{GC}=\frac{EH}{GB}$,
∴$\frac{DH}{EH}=\frac{GC}{BG}$,
由(1)得:$\frac{DH}{HE}=\frac{BG}{GC}$,
∴$\frac{GC}{BG}=\frac{BG}{GC}$,
∴BG=CG,即点G是BC的中点;
(2)解:如图所示,直线MO1即为所求.
点评 本题是相似形综合题目,考查了相似三角形的判定与性质、矩形的性质,正确根据相似三角形的对应边的比相等,通过等量代换得到$\frac{GC}{BG}=\frac{BG}{GC}$是解决问题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1. 如图,直线a、b被直线c所截,a∥b,∠1=∠2,若∠4=65°,则∠3等于( )
如图,直线a、b被直线c所截,a∥b,∠1=∠2,若∠4=65°,则∠3等于( )
 如图,直线a、b被直线c所截,a∥b,∠1=∠2,若∠4=65°,则∠3等于( )
如图,直线a、b被直线c所截,a∥b,∠1=∠2,若∠4=65°,则∠3等于( )| A. | 30° | B. | 50° | C. | 65° | D. | 115° |
18.计算$\sqrt{12}-3\sqrt{3}$的结果是( )
| A. | 1 | B. | -1 | C. | $\sqrt{3}$ | D. | $-\sqrt{3}$ |
15.∠α=35°,则∠α的余角的度数为( )
| A. | 65° | B. | 55° | C. | 45° | D. | 25° |
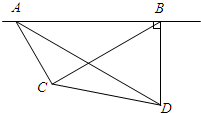 如图,在我市的上空一架飞机由A向B沿水平直线方向飞行,沿航线AB的正下方有两个景点水城明珠大剧院(记为点C),光岳楼(记为点D),飞机在A处时,测得景点C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了3千米到B处时,往后测得景点C的俯角为30°.而景点D恰好在飞机的正下方,求水城明珠大剧院与光岳楼之间的距离(最后结果精确到0.1千米)
如图,在我市的上空一架飞机由A向B沿水平直线方向飞行,沿航线AB的正下方有两个景点水城明珠大剧院(记为点C),光岳楼(记为点D),飞机在A处时,测得景点C、D在飞机的前方,俯角分别为60°和30°.飞机飞行了3千米到B处时,往后测得景点C的俯角为30°.而景点D恰好在飞机的正下方,求水城明珠大剧院与光岳楼之间的距离(最后结果精确到0.1千米)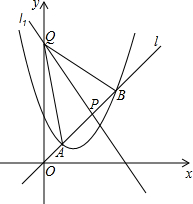 已知抛物线C:y=x2-3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.
已知抛物线C:y=x2-3x+m,直线l:y=kx(k>0),当k=1时,抛物线C与直线l只有一个公共点.