题目内容
4.如图1,这是由8个同样大小的立方体组成的魔方,体积为64.(1)求出这个魔方的棱长.
(2)图中阴影部分是一个正方形ABCD,求出阴影部分的面积及其边长.
(3)把正方形ABCD放到数轴上,如图2,使得A与-1重合,那么D在数轴上表示的数为-1-2$\sqrt{2}$.
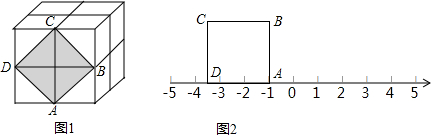
分析 (1)根据正方体的体积格式可求这个魔方的棱长.
(2)根据魔方的棱长为4,所以小立方体的棱长为2,阴影部分由4个直角三角形组成,算出一个直角三角形的面积乘以4即可得到阴影部分的面积,开平方即可求出边长.
(3)根据两点间的距离公式可得D在数轴上表示的数.
解答 解:(1)$\root{3}{64}=4$.
答:这个魔方的棱长为4.
(2)∵魔方的棱长为4,
∴小立方体的棱长为2,
∴阴影部分面积为:$\frac{1}{2}$×2×2×4=8,
边长为:$\sqrt{8}$=2$\sqrt{2}$.
答:阴影部分的面积是8,边长是2$\sqrt{2}$.
(3)D在数轴上表示的数为-1-2$\sqrt{2}$.
故答案为:-1-2$\sqrt{2}$.
点评 本题考查的是立方根在实际生活中的运用,解答此题的关键是根据立方根求出魔方的棱长.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
15.下列运算中正确的是( )
| A. | $\sqrt{16}$=±4 | B. | 100${\;}^{-\frac{1}{2}}$=-10 | C. | $\root{4}{(-3)^{4}}$=-3 | D. | |$\sqrt{8}$-3|=3-$\sqrt{8}$ |
19.下列运算正确的是( )
| A. | $\sqrt{8}$-$\sqrt{2}$=$\sqrt{2}$ | B. | $\sqrt{4\frac{1}{9}}$=2$\frac{1}{3}$ | C. | $\sqrt{5}$-$\sqrt{3}$=$\sqrt{2}$ | D. | $\sqrt{(2-\sqrt{5})^{2}}$=2-$\sqrt{5}$ |
9.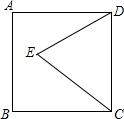 如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
 如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )
如图,正方形ABCD的边长为6,以CD为一边作等边三角形△DCE,点E在正方形内部,则点E到CD的距离是( )| A. | 6 | B. | 3$\sqrt{3}$ | C. | 2 | D. | 2$\sqrt{3}$ |
16.已知等腰三角形两边长分别为3和5,第三边是方程x2-5x+6=0的解,则这个三角形的周长是( )
| A. | 9 | B. | 10 | C. | 11 | D. | 14 |
13.下列计算正确的是( )
| A. | 3a2-a2=2 | B. | a6•a3=a18 | C. | (a3)3=a6 | D. | x3÷x-1=x4 |
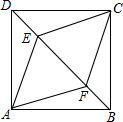 正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.
正方形ABCD中,点E,F是对角线BD上的两点,且DE=BF.