题目内容
8.已知a=|x-y|,b=x-y,c=y-x.(1)若x=5,y=3,试分别计算a、b、c的值;
(2)当x≥y时,试说明a、b、c之间的数量关系;
(3)当x<y时,试比较a+b与c的大小.
分析 (1)将x=5,y=3代入计算即可;
(2)由x≥y,化简绝对值,然后可得到答案;
(3)由x<y化简绝对值,然后再求得a+b与c,最后比较大小即可.
解答 解:(1)若x=5,y=3则a=|5-3|=2,b=x-y=2,c=y-x=-2;
(2)当x≥y时,a=x-y,所以a=b=-c;
(3)当x<y时,a=y-x,a+b=0,y-x>0,所以a+b<c.
点评 本题主要考查的是求代数式的值、绝对值的性质、比较代数式的大小,熟练掌握绝对值的性质是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.下列方程:①x2=0,②$\frac{1}{x^2}$-2=0,③2x2+3x=(1+2x)(2+x),④$\frac{{2{x^3}}}{x}$-8x+1=0中,一元二次方程的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.已知a,b互为相反数,则下列各组数中不是互为相反数的是( )
| A. | -2a和-2b | B. | 2a和2b | C. | a+1和b+1 | D. | a+1和b-1 |
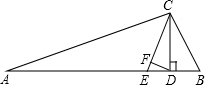 △ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°.
△ABC中,CD⊥AB于D,CE是∠ACB的平分线,∠A=20°,∠B=60°. 已知:如图,AB∥CD,AB=CD,求证:AD∥BC.
已知:如图,AB∥CD,AB=CD,求证:AD∥BC.