题目内容
7.抛物线y=-$\frac{1}{2}$(x+1)2,y=-$\frac{1}{2}$(x-1)2与抛物线y=-$\frac{1}{2}$x2有什么关系?分析 利用描点法分别得出函数y=-$\frac{1}{2}$(x+1)2,y=-$\frac{1}{2}$(x-1)2,y=-$\frac{1}{2}$x2的图象,利用所画图象得出它们之间的关系.
解答 解:如图所示: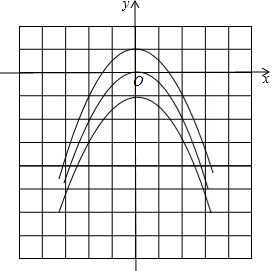
由图象可知函数y=-$\frac{1}{2}$(x+1)2,y=-$\frac{1}{2}$(x-1)2与抛物线y=-$\frac{1}{2}$x2的图象,共同点:形状相同,开口方向向下,对称轴是y轴;
不同点是:它们的顶点不同;抛物线y=-$\frac{1}{2}$(x+1)2向下平移一个单位得到抛物线y=-$\frac{1}{2}$x2,抛物线y=-$\frac{1}{2}$x2向下平移一个单位得到y=-$\frac{1}{2}$(x-1)2.
点评 此题主要考查了二次函数的图象画法以及二次函数的性质,利用描点法画出函数图象是解题关键.

练习册系列答案
相关题目
17.第29届北京奥运会火炬接力活动历时130天,传递行程约为137000km,用科学记数法表示是( )
| A. | 13.7×103km | B. | 13.7×104km | C. | 1.37×105km | D. | 0.137×106km |
 如图,三根等长的筷子AB、AC、AD放在桌面上,用粉笔连接BC、CD、BD,求证:β=2θ.
如图,三根等长的筷子AB、AC、AD放在桌面上,用粉笔连接BC、CD、BD,求证:β=2θ.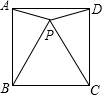 如图,等边△BCP在正方形ABCD内,则∠APD=150度.
如图,等边△BCP在正方形ABCD内,则∠APD=150度.