题目内容
8.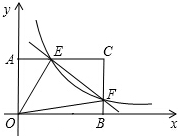 在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)图象与AC边交于点E.
在矩形AOBC中,OB=6,OA=4,分别以OB,OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上一点(不与B、C两点重合),过点F的反比例函数y=$\frac{k}{x}$(k>0)图象与AC边交于点E.(1)请用k表示点E,F的坐标;
(2)若△OEF的面积为9,求反比例函数的解析式.
分析 (1)易得E点的纵坐标为4,F点的横坐标为6,把它们分别代入反比例函数y=$\frac{k}{x}$(k>0)即可得到E点和F点的坐标;
(2)分别用矩形面积和能用图中的点表示出的三角形的面积表示出所求的面积,解方程即可求得k的值.
解答 解:(1)E( $\frac{k}{4}$,4),F(6,$\frac{k}{6}$);
(2)∵E,F两点坐标分别为E( $\frac{k}{4}$,4),F(6,$\frac{k}{6}$),
∴S△ECF=$\frac{1}{2}$EC•CF=$\frac{1}{2}$(6-$\frac{1}{4}$k)(4-$\frac{1}{6}$k),
∴S△EOF=S矩形AOBC-S△AOE-S△BOF-S△ECF
=24-$\frac{1}{2}$k-$\frac{1}{2}$k-S△ECF
=24-k-$\frac{1}{2}$(6-$\frac{1}{4}$k)(4-$\frac{1}{6}$k),
∵△OEF的面积为9,
∴24-k-$\frac{1}{2}$(6-$\frac{1}{4}$k)(4-$\frac{1}{6}$k)=9,
整理得,$\frac{{k}^{2}}{24}$=6,
解得k=12.
∴反比例函数的解析式为y=$\frac{12}{x}$.
点评 本题考查了反比例函数的性质和图形的面积计算;点在反比例函数图象上,则点的横纵坐标满足其解析式;在求坐标系内一般三角形的面积,通常整理为矩形面积减去若干直角三角形的面积的形式.

练习册系列答案
相关题目
18.下列各式为最简二次根式的是( )
| A. | $\sqrt{8}$ | B. | $\frac{\sqrt{15}}{2}$ | C. | $\sqrt{\frac{2}{3}}$ | D. | $\frac{\sqrt{12}}{5}$ |
13.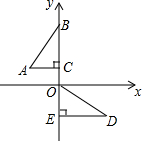 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
 如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )
如图,在平面直角坐标系中,点B、C、E、在y轴上,Rt△ABC经过变换得到Rt△ODE.若点C的坐标为(0,1),AC=2,则这种变换可以是( )| A. | △ABC绕点C顺时针旋转90°,再向下平移3 | |
| B. | △ABC绕点C顺时针旋转90°,再向下平移1 | |
| C. | △ABC绕点C逆时针旋转90°,再向下平移1 | |
| D. | △ABC绕点C逆时针旋转90°,再向下平移3 |
17.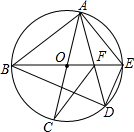 如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
 如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )
如图,AC,BE是⊙O的直径,弦AD与BE交于点F,下列三角形中,外心不是点O的是( )| A. | △ABE | B. | △ACF | C. | △ABD | D. | △ADE |
18.计算:cos245°+sin245°=( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{2}}{2}$ |
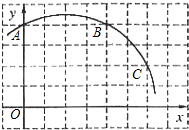 如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.
如图,已知直角坐标系中一条圆弧经过正方形网格的格点A、B、C.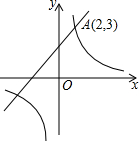 如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为y1>y2.
如图,一次函数y1=k1x+b(k1、b为常数,且k1≠0)的图象与反比例函数y2=$\frac{{k}_{2}}{x}$(k2为常数,且k2≠0)的图象都经过点A(2,3).则当x>2时,y1与y2的大小关系为y1>y2.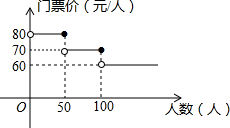 我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.
我市某风景区门票价格如图所示,黄冈赤壁旅游公司有甲、乙两个旅游团队,计划在“五一”小黄金周期间到该景点游玩.两团队游客人数之和为120人,乙团队人数不超过50人,设甲团队人数为x人.如果甲、乙两团队分别购买门票,两团队门票款之和为W元.