若y=$\frac{\sqrt{9-x}+\sqrt{x-9}+3}{x}$.则5x+6y的值为47．题目和参考答案——青夏教育精英家教网—

题目内容

15．若y=$\frac{\sqrt{9-x}+\sqrt{x-9}+3}{x}$，则5x+6y的值为47．

分析根据二次根式有意义的条件即可求出x与y的值．

解答解：由题意可知：$\left\{\begin{array}{l}{9-x≥0}\\{x-9≥0}\end{array}\right.$，
∴$\left\{\begin{array}{l}{x≤9}\\{x≥9}\end{array}\right.$
∴x=9，
∴y=$\frac{3}{9}$=$\frac{1}{3}$
∴5x+6y=47
答故案为：47

点评本题考查二次根式有意义的条件，解题的关键是正确理解二次根式有意义的条件，本题属于基础题型．

练习册系列答案

相关题目

16．

实数a，b，c在数轴上的对应点的位置如图所示，则a的相反数是（　　）

17．9的平方根是±3；9的立方根是$\root{3}{9}$．

3．

如图，在边长为1的小正方形构成的网格中，有一个半径为1的⊙O，且圆心在格点上，tan∠AED的值为$\frac{1}{2}$．

$\frac{{a}^{6}}{{a}^{2}}$=a³

C．

$\frac{-a-b}{a+b}$=-1

7．

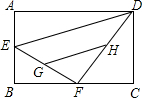如图，在矩形ABCD中，AB=4，AD=6，点E是AB的中点，点F是BC边上的动点，连接EF，DF，G，H分别是EF和DF的中点，则GH的长为$\sqrt{10}$．

4．化简求值：[（x+y）（x-y）-（x-y）²+2y（x-y）]÷4y，其中x=1，y=2．

5．

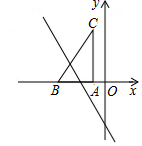如图，把Rt△ABC放在直角坐标系内，其中∠CAB=90°，BC=5，点A，B的坐标分别为（-1，0），（-4，0），将△ABC沿x轴向左平移，当点C落在直线y=-2x-6上时，则点C沿x轴向左平移了4个单位长度．

试题分类