��Ŀ����
8����ͼ����ƽ��ֱ������ϵ�У���֪��A��-1��$\frac{3}{4}$����B��2��0����������11��y=ax2+bx+1��a��bΪ��������a��0���ϣ�ֱ��12����������11�Ķ�������y�ᴹֱ������Ϊ��D����1����l1�Ľ���ʽ����д�����ĶԳ���Ͷ������ꣻ
��2����l1����һ����P�ӵ�A�������������ߴ��������˶�����P��������ypҲ��֮��ÿ��2����λ�����ٶȱ仯�����P�˶���ʱ��Ϊt���룩������OP�����߶�OPΪֱ������F��
����yp����t�ı���ʽ����д��t��ȡֵ��Χ��
�ڵ���P�����A��ʱ��ֱ��l2���F��λ�ù�ϵ�����У��ڵ�P�ӵ�A�˶�����D�Ĺ����У�ֱ��12���F�Ƿ�ʼ�ձ�����������λ�ù�ϵ����˵�����ɣ�
��3���ڣ�2�������£�����P��ʼ�ӵ�A�������������ߴ������˶�ʱ��ֱ��l2ͬʱ����ƽ�ƣ�����D��������yD��ÿ��3����λ�����ٶȱ仯����ֱ��l2���F�ཻʱ����t��ȡֵ��Χ��

���� ��1����A��-1��$\frac{3}{4}$����B��2��0���������������y=ax2+bx+1����ʽ���з����鼴�ɽ�����⣮
��2���ٷ������������ۢ�0��t��$\frac{1}{8}$����t��$\frac{1}{8}$���ֱ���⼴�ɣ��ڵ���P�����A��ʱ��ֱ��l2���F��λ�ù�ϵ�����У����ۣ��ڵ�P�ӵ�A�˶�����D�Ĺ����У�ֱ��12���Fʼ�ձ������У�ֻҪ���Բ�ĵ�ֱ��y=1�ľ��룬�Լ�Բ�İ뾶�����жϣ�
��3���տ�ʼʱֱ��l2���F�����еģ����������ཻ�ģ�ֻҪ����ڶ�������ʱ��ʱ�伴�ɽ�����⣮
��� �⣺��1���ѵ�A��-1��$\frac{3}{4}$����B��2��0������������11��y=ax2+bx+1�еã�
$\left\{\begin{array}{l}{a-b+1=\frac{3}{4}}\\{4a+2b+1=0}\end{array}\right.$ ���$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{b=0}\end{array}\right.$��
��y=-$\frac{1}{4}$x2+1 ��Գ���Ϊ��ֱ��x=0������Ϊ��0��1����
��2����������1-$\frac{3}{4}$=2t���t=$\frac{1}{8}$��
��0��t$��\frac{1}{8}$ʱ��yP=$\frac{3}{4}$+2t��
t��$\frac{1}{8}$ʱ��yP=1-2��t-$\frac{1}{8}$��=$\frac{5}{4}$-2t��
�ڵ���P�����A��ʱ��OA=$\sqrt{{1}^{2}+��\frac{3}{4}��^{2}}$=$\frac{5}{4}$��
���F�İ뾶Ϊ$\frac{5}{8}$��
�ߵ�F���꣨-$\frac{1}{2}$��$\frac{3}{8}$����
���F��ֱ��y=1�ľ���Ϊ$\frac{8}{5}$��
���F��ֱ��y=1�ľ�����ڡ�F�İ뾶��
��ֱ��l2���F���У�
�ʴ�Ϊ���У�
���ۣ��ڵ�P�ӵ�A�˶�����D�Ĺ����У�ֱ��12���Fʼ�ձ������У�
���ɣ����P���꣨m��-$\frac{1}{4}$m2+1�������F���꣨$\frac{1}{2}$m��-$\frac{1}{8}$m2+$\frac{1}{2}$����
��OP=$\sqrt{{m}^{2}+��-\frac{1}{4}{m}^{2}+1��^{2}}$=$\frac{1}{4}$m2+1��
���F�İ뾶=$\frac{1}{8}$m2+$\frac{1}{2}$��
�ߵ�F��ֱ��y=1�ľ���Ϊ1-��-$\frac{1}{8}$m2+$\frac{1}{2}$��=$\frac{1}{8}$m2+$\frac{1}{2}$��
���F��ֱ��y=1�ľ�����ڡ�F�İ뾶��
���ڵ�P�ӵ�A�˶�����D�Ĺ����У�ֱ��12���Fʼ�ձ������У�
��3�����P���꣨m��-$\frac{1}{4}$m2+1�������F���꣨$\frac{1}{2}$m��-$\frac{1}{8}$m2+$\frac{1}{2}$����
��OP=$\sqrt{{m}^{2}+��-\frac{1}{4}{m}^{2}+1��^{2}}$=$\frac{1}{4}$m2+1��
���F�İ뾶=$\frac{1}{8}$m2+$\frac{1}{2}$��
��ֱ��y=-$\frac{1}{8}$m2+$\frac{1}{2}$-��$\frac{1}{8}$m2+$\frac{1}{2}$��=-$\frac{1}{4}$m2���F���У�
��t��$\frac{1}{8}$ʱ��-$\frac{1}{4}$m2+1=1-2��t-$\frac{1}{8}$����
��-$\frac{1}{4}$m2=-2t+$\frac{1}{4}$��
��1-3t=-2t+$\frac{1}{4}$ʱֱ��l2���F���У����t=$\frac{3}{4}$��
�൱0��t��$\frac{3}{4}$ʱ����F��ֱ��l2�ཻ��
���� ���⿼����κ����ۺ��⡢ֱ����Բ��λ�ù�ϵ���������빫ʽ�����ɶ�����֪ʶ������Ĺؼ����������빫ʽ��Ӧ�ã�������ת��Ϊ����ȥ˼����ѧ����������λ�ý�����⣬�����п�ѹ���⣮

| A�� | x2-2�Ƕ��ζ���ʽ | |
| B�� | ����ʽ-x2��ϵ����1 | |
| C�� | ʹʽ��$\sqrt{x+2}$�������x��ȡֵ��Χ��x��-2 | |
| D�� | ����ʽ$\frac{{a}^{2}-1}{a+1}$��ֵ����0����a=��1 |
 ������L��y=ax2+bx+c��a��0��a��b��cΪ�������Ķ���Ϊԭ�㣬�Ҿ�����A��2$\sqrt{a}$��$\frac{1}{4}$����ֱ��y=kx+1��y�ύ�ڵ�F����������L����B��x1��y1����C��x2��y2�����㣨����x1��x2������ֱ��l��y=-1������ΪM������AF��
������L��y=ax2+bx+c��a��0��a��b��cΪ�������Ķ���Ϊԭ�㣬�Ҿ�����A��2$\sqrt{a}$��$\frac{1}{4}$����ֱ��y=kx+1��y�ύ�ڵ�F����������L����B��x1��y1����C��x2��y2�����㣨����x1��x2������ֱ��l��y=-1������ΪM������AF��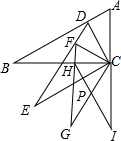 ��ͼ��Rt��ABC�У���B=30�㣬��ACB=90�㣬CD��AB��AB��D����CDΪ�϶̵�ֱ�DZ����CDB��ͬ����Rt��DEC�������E=30�㣬��DCE=90�㣬����ͬ���ķ�����Rt��FGC����FCG=90�㣬������ͬ���ķ�����Rt��HIC����HCI=90�㣮��AC=a����CI�ij���
��ͼ��Rt��ABC�У���B=30�㣬��ACB=90�㣬CD��AB��AB��D����CDΪ�϶̵�ֱ�DZ����CDB��ͬ����Rt��DEC�������E=30�㣬��DCE=90�㣬����ͬ���ķ�����Rt��FGC����FCG=90�㣬������ͬ���ķ�����Rt��HIC����HCI=90�㣮��AC=a����CI�ij���