题目内容
15.(1)计算:$(a+\frac{1}{a+2})÷(a-2+\frac{3}{a+2})$(2)解方程:$\frac{1-2x}{x-2}=2+\frac{3}{2-x}$.
分析 (1)原式先计算括号中的运算,再计算除法运算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=$\frac{{a}^{2}+2a+1}{a+2}$÷$\frac{{a}^{2}-1}{a+2}$=$\frac{(a+1)^{2}}{a+2}$•$\frac{a+2}{(a+1)(a-1)}$=$\frac{a+1}{a-1}$;
(2)去分母得:1-2x=2x-4-3,
解得:x=2,
经检验x=2是增根,原方程无解.
点评 此题考查了解分式方程,利用了转化的思想,解分式方程注意要检验.

练习册系列答案
相关题目
7.下列各式不是一元一次不等式组的是( )
| A. | $\left\{\begin{array}{l}x>3\\ x<1\end{array}\right.$ | B. | $\left\{\begin{array}{l}3x<5\\ 2x-1<9\end{array}\right.$ | C. | $\left\{\begin{array}{l}x-1>3\\ y+2<1\end{array}\right.$ | D. | $\left\{\begin{array}{l}x-1>3\\ x-3<2\end{array}\right.$ |
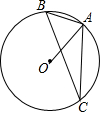 如图,A、B、C是⊙O上三点,∠OAB=65°,则∠ACB的度数是25°.
如图,A、B、C是⊙O上三点,∠OAB=65°,则∠ACB的度数是25°.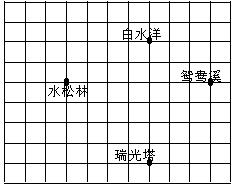 暑假时小明和小颖到福建屏南旅游,小明在如上图所示的旅游简图上建立了直角坐标系,但他只告诉小颖白水洋的坐标是(2,5),请你帮小颖写出鸳鸯溪的坐标是(5,3).
暑假时小明和小颖到福建屏南旅游,小明在如上图所示的旅游简图上建立了直角坐标系,但他只告诉小颖白水洋的坐标是(2,5),请你帮小颖写出鸳鸯溪的坐标是(5,3).