题目内容
6.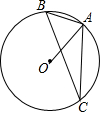 如图,A、B、C是⊙O上三点,∠OAB=65°,则∠ACB的度数是25°.
如图,A、B、C是⊙O上三点,∠OAB=65°,则∠ACB的度数是25°.
分析 连接OB,根据等腰三角形的性质和三角形内角和定理求出∠AOB,根据圆周角定理计算即可.
解答  解连接OB,
解连接OB,
∵OA=OB,
∴∠OBA=∠OAB=65°,
∴∠AOB=50°,
由圆周角定理得,∠ACB=$\frac{1}{2}$∠AOB=25°,
故答案为:25°.
点评 本题考查的是圆周角定理的应用,掌握在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半是解题的关键.

练习册系列答案
相关题目
14. 如图,已知∠1=∠2,则下列结论一定正确的是( )
如图,已知∠1=∠2,则下列结论一定正确的是( )
 如图,已知∠1=∠2,则下列结论一定正确的是( )
如图,已知∠1=∠2,则下列结论一定正确的是( )| A. | ∠3=∠4 | B. | AB∥CD | C. | AD∥BC | D. | ∠B=∠D |
18.下列判断正确的是( )
| A. | 两条直线被第三条直线所截,同位角相等 | |
| B. | 在同一平面内,a⊥b,b⊥c,则c⊥a | |
| C. | 同旁内角互补,则它们的角平分线互相垂直 | |
| D. | 经过一点有且只有一条直线与已知直线平行 |
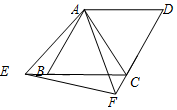 如图,把两个边长相等的等边△ABC和△ACD拼成菱形ABCD,点E、F分别是射线CB、DC上的动点(E、F与B、C、D不重合),且始终保持BE=CF,连结AE、AF、EF.
如图,把两个边长相等的等边△ABC和△ACD拼成菱形ABCD,点E、F分别是射线CB、DC上的动点(E、F与B、C、D不重合),且始终保持BE=CF,连结AE、AF、EF. 如图,已知∠1+∠2=180°,∠3=108°.求∠4的度数.
如图,已知∠1+∠2=180°,∠3=108°.求∠4的度数.