题目内容
大冶市A、B两个蔬菜基地得知C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
(2)设总运费为W,求W与x之间的函数关系式,并求出当x为多少时,W最小.
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调运方案.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
(2)设总运费为W,求W与x之间的函数关系式,并求出当x为多少时,W最小.
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调运方案.
| C | D | 总计 | |
| A | 200吨 | ||
| B | x吨 | 300吨 | |
| 总计 | 240吨 | 260吨 | 500吨 |
考点:一次函数的应用
专题:
分析:(1)根据题意可得:从B地运往C处的蔬菜为x吨,则从B地运往D处的蔬菜为(300-x)吨,从A地运往C处的蔬菜为(240-x)吨,从A地运往D处的蔬菜为[200-(240-x)]=(x-40)吨,根据运费相等列方程解答;
(2)利用(1)中对应运的吨数,然后分别乘以运费得到总运费,即W=(240-x)×20+(x-40)]×25+15x+(300-x)×18=2x+9200,再利用运往各地的蔬菜都为非负数可得到x的取值范围;由于W=2x+9200,根据一次函数性质得到k=2>0,则y随x的增大而增大,在x的范围内取最小值.
(3)根据B地到C处的运费每吨减少m元,列出总运费W=(240-x)×20+(x-40)]×25+(15-m)x+(300-x)×18=(2-m)x+9200,把(2)中的数值代入,进一步由探讨m的值得出答案即可.
(2)利用(1)中对应运的吨数,然后分别乘以运费得到总运费,即W=(240-x)×20+(x-40)]×25+15x+(300-x)×18=2x+9200,再利用运往各地的蔬菜都为非负数可得到x的取值范围;由于W=2x+9200,根据一次函数性质得到k=2>0,则y随x的增大而增大,在x的范围内取最小值.
(3)根据B地到C处的运费每吨减少m元,列出总运费W=(240-x)×20+(x-40)]×25+(15-m)x+(300-x)×18=(2-m)x+9200,把(2)中的数值代入,进一步由探讨m的值得出答案即可.
解答:解:(1)填表
∵运费相等,
∴依题意得:20(240-x)+25(x-40)=15x+18(300-x).
解得:x=200.
(2)w与x之间的函数关系为:w═(240-x)×20+(x-40)]×25+15x+(300-x)×18=2x+9200,
依题意得:
,
∴40≤x≤240,
在w=2x+9200中,
∵2>0,
∴w随x的增大而增大,
故当x=40时,总运费最小,
(3)由题意得W=(240-x)×20+(x-40)]×25+(15-m)x+(300-x)×18=(2-m)x+9200,
∴0<m<2时,(2)中调运方案总运费最小;
m=2时,在40≤x≤240的前提下调运
方案的总运费不变;
2<m<15时,x=240总运费最小,
其调运方案如表二:
| C | D | 总计 | |
| A | (240-x)吨 | (x-40)吨 | 200吨 |
| B | x吨 | (300-x)吨 | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
∴依题意得:20(240-x)+25(x-40)=15x+18(300-x).
解得:x=200.
(2)w与x之间的函数关系为:w═(240-x)×20+(x-40)]×25+15x+(300-x)×18=2x+9200,
依题意得:
|
∴40≤x≤240,
在w=2x+9200中,
∵2>0,
∴w随x的增大而增大,
故当x=40时,总运费最小,
(3)由题意得W=(240-x)×20+(x-40)]×25+(15-m)x+(300-x)×18=(2-m)x+9200,
∴0<m<2时,(2)中调运方案总运费最小;
m=2时,在40≤x≤240的前提下调运
方案的总运费不变;
2<m<15时,x=240总运费最小,
其调运方案如表二:
| C | D | |
| A | 0吨 | 200吨 |
| B | 240吨 | 60吨 |
点评:本题考查了一次函数的应用:根据实际问题列出一次函数关系,然后利用一次函数的性质解决问题.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
已知实数x、y满足2
+3(y+1)2=0,则x-y=( )
| x-2 |
| A、3 | B、-3 | C、1 | D、-1 |

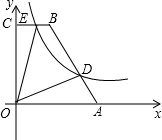 如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y=
如图,在直角梯形OABC中,BC∥AO,∠AOC=90°,点A,B的坐标分别为(5,0),(2,6),点D为AB上一点,且BD=2AD,双曲线y=
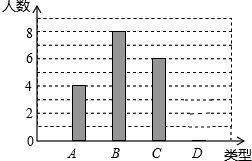 某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题:
某校240名学生参加植树活动,要求每人植树4~7棵,活动结束后抽查了20名学生每人的植树量,并分为四类:A类4棵、B类5棵、C类6棵、D类7棵,将各类的人数绘制成如图所示不完整的条形统计图,回答下列问题: