题目内容
如图，在三角形ABC中，AC=BC，若将△ABC沿BC方向向右平移BC长的距离，得到△CEF，连接AE．
（1）试猜想，AE与CF有何位置上的关系？并对你的猜想给予证明；
（2）若BC=10，tan∠ACB=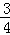
时，求AB的长．
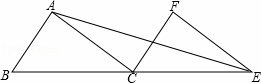
解：（1）AE⊥CF
证明：如图，连接AF，
∵AC=BC，
又∵△ABC沿BC方向向右平移BC长的距离，
∴AC=CE=EF=AF．
∴四边形ACEF是菱形．
∴AE⊥CF．
（2）如图，作AD⊥BC于D．
∵tan∠AC
B=
，
设AD=3KDC=4K，
在Rt△ADC中，AC=10，
∵AD2+DC2=AC2
∴K=2．
∴AD=6cm，DC=8cm．
∴BD=2cm．
在Rt△ADB中，根据勾股定理：AB=2
cm．
练习册系列答案
相关题目
接触
到点P时停止倒入．图2是它的平面示意图，请根据图中的信息，求出容器中牛奶的高度（结果精确到0.1cm）．（参考数据：
≈1.73，
≈1.41）
的是（ ）
