题目内容
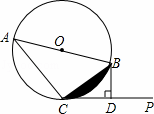
如图,AB是⊙O的直径,点C在⊙O上,CD与⊙O相切,BD∥AC.
(1)图中∠OCD= °,理由是 ;
(2)⊙O的半径为3,AC=4,求CD的长.
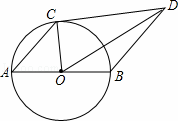
解:(1)∵CD与⊙O相切,
∴OC⊥CD,(圆的切线垂直于经过切点的半径)
∴∠OCD=90°;
故答案是:90,圆的切线垂直于经过切点的半径;
(2)连接BC.
∵BD∥AC,
∴∠CBD=∠OCD=90°,
∴在直角△ABC中,
BC= =
= =2
=2 ,
,
∠A+∠ABC=90°,
∵OC=OB,
∴∠BCO=∠ABC,
∴∠A+∠BCO=90°,
又∵∠OCD=90°,
即∠BCO+∠BCD=90°,
∴∠BCD=∠A,
又∵∠CBD=∠ACB,
∴△ABC∽△CDB,
∴ =
= ,
,
∴ =
= ,
,
解得:CD=3 .
.


练习册系列答案
相关题目
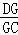 =
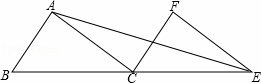
=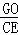 ;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )
;④(a﹣b)2•S△EFO=b2•S△DGO.其中结论正确的个数是( )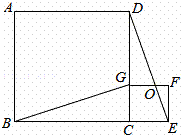
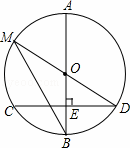


 B.
B. C.
C. D.
D. 


 B.
B. C.
C. D.
D. 
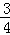 时,求AB的长.
时,求AB的长.