题目内容
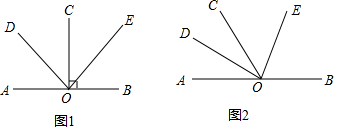
12.已知点O在直线AB上,OD平分∠AOC,OE平分∠BOC.(1)若OC⊥AB于点O,如图1,直接写出∠DOE的度数为90°;OD与OE的位置关系是垂直;
(2)若OC与AB不垂直,如图2,其它条件不变,(1)中的结论还成立吗?若成立,请说明你的猜想是正确的;若不成立,请说明理由;
(3)如图2,若∠AOD=40°,请你利用(2)中得到的结论,求∠BOE的度数.
分析 (1)先根据角平分线的性质得出∠DOC与∠EOC的度数,进而可得出结论;
(2)根据角平分线的性质即可得出结论;
(3)根据(2)的规律可直接得出结论.
解答 解:(1)∵CO⊥AB于点O,OD平分∠AOC,OE平分∠BOC,
∴∠COD=$\frac{1}{2}$∠AOC=45°,∠COE=$\frac{1}{2}$∠BOC=45°,
∴∠DOE=45°+45°=90°,
∴OD⊥OE.
故答案为:90°,垂直;
(2)成立.
∵OD平分∠AOC,OE平分∠BOC,
∴∠COD=$\frac{1}{2}$∠AOC,∠COE=$\frac{1}{2}$∠BOC,
∵∠AOC+∠BOC=180°,
∴∠COD+∠COE=$\frac{1}{2}$(∠AOC+∠BOC)=90°;
(3)∵∠AOD=40°,
∴∠BOE=90°-40°=50°.
点评 本题考查的是角平分线的定义,熟知从一个角的顶点出发,把这个角分成相等的两个角的射线叫做这个角的平分线是解答此题的关键.

练习册系列答案
相关题目
2.计算(2x-1)2等于( )
| A. | 4x2+1 | B. | 4x2-2x+1 | C. | 4x2-4x-1 | D. | 4x2-4x+1 |
20. 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
 如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )
如图,三条直线l1,l2,l3相交于点O,则∠1+∠2+∠3=( )| A. | 180° | B. | 150° | C. | 120° | D. | 90° |
 如图,C是线段AB的中点,D是线段AC的中点,已知线段CD=3cm,则线段AB=cm12.
如图,C是线段AB的中点,D是线段AC的中点,已知线段CD=3cm,则线段AB=cm12.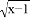 有意义,那么x的取值范围是( )
有意义,那么x的取值范围是( )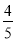 B.
B. 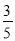 C.
C. 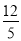 D.
D.