题目内容
16.已知关于x的一元二次方程x2-2x+a-1=0的两个实数根分别为x1,x2,且满足$\frac{1}{{x}_{1}}$$+\frac{1}{{x}_{2}}$=-$\frac{2}{3}$,求a的值.分析 根据根与系数的关系即可得出x1+x2=2、x1•x2=a-1,将$\frac{1}{{x}_{1}}$$+\frac{1}{{x}_{2}}$通分后可得出$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$,代入数值即可得出关于a的分式方程,解之即可得出结论.
解答 解:∵关于x的一元二次方程x2-2x+a-1=0的两个实数根分别为x1,x2,
∴x1+x2=2,x1•x2=a-1.
∵$\frac{1}{{x}_{1}}$$+\frac{1}{{x}_{2}}$=$\frac{{x}_{1}+{x}_{2}}{{x}_{1}•{x}_{2}}$=$\frac{2}{a-1}$=-$\frac{2}{3}$,
∴a=-2,
经检验,a=-2是方程$\frac{2}{a-1}$=-$\frac{2}{3}$的解.
∴a的值为-2.
点评 本题考查了根与系数的关系以及解分式方程,根据根与系数的关系结合$\frac{1}{{x}_{1}}$$+\frac{1}{{x}_{2}}$=-$\frac{2}{3}$找出关于a的分式方程是解题的关键.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
7.下列各式是一元一次方程的是( )
| A. | x+3y=4 | B. | x2-2x=6 | C. | -6x=0 | D. | x-1═$\frac{1}{x}$ |
11.若a<0,则|a|的相反数是( )
| A. | $\frac{1}{a}$ | B. | -$\frac{1}{a}$ | C. | a | D. | -a |
8.某公司今年4月分营业额为60万元,6月份营业额达到100万元,设该公司5,6两个月营业额的月平均增长率为x,则下列方程中正确的是( )
| A. | 60(1+2x)=100 | B. | 100(1+x)2=60 | ||
| C. | 60(1+x)2=100 | D. | 60+60(1+x)+60(1+x)2=100 |
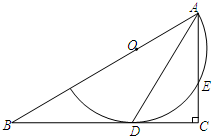 如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.
如图,△ABC中,∠C=90°,点O为AB上的一点,以点O为圆心,OA为半径的圆弧与BC相切于点D,交AC于点E,连接AD.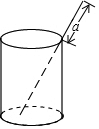 如图,将一根长18cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是5≤a≤6.
如图,将一根长18cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是5≤a≤6.