题目内容
6.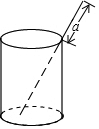 如图,将一根长18cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是5≤a≤6.
如图,将一根长18cm的筷子,置于底面直径为5cm,高为12cm的圆柱形茶杯中,设筷子露在杯子外面的长为acm(茶杯装满水),则a的取值范围是5≤a≤6.
分析 根据题意可知当筷子竖直放置时,露出杯子外面的部分最长,当筷子斜着插入底部时最短,从而可以求得a的取值范围.
解答 解:由题意可得,
当筷子竖直放置时,露出杯子外面的部分最长,此时a=18-12=6,
当筷子斜着插入底部时最短,此时a=18-$\sqrt{1{2}^{2}+{5}^{2}}$=18-13=5,
故a的取值范围是5≤a≤6,
故答案为:5≤a≤6.
点评 本题考查勾股定理的应用,解答此类问题的关键是明确题意,找出所求问题需要的条件,利用勾股定理解答.

练习册系列答案
相关题目
17.下列方程是一元一次方程的是( )
| A. | x-2=3 | B. | 1+5=6 | C. | x2+x=1 | D. | x-3y=0 |
1.2016年5月25日,邯郸市中考报名工作已结束,全市中考报名总人数比2015年的增长15%还多1335人,若2015年邯郸市中考有a人报名,则2016年邯郸市中考报名的总人数为( )
| A. | [(1+15%)a+1335]人 | B. | [(1-15%)a+1335]人 | C. | 15%(a+1335)人 | D. | (15%-1335)人 |
15.下列方程是一元二次方程的是( )
| A. | 3x2-7=5y+1 | B. | $\frac{\sqrt{5}}{3}$x-$\sqrt{3}$=$\frac{1}{2}$x2+x | ||
| C. | 2x2-7y-2=0 | D. | 3x2-5x+7=3x2+6x-4 |
16.下列运算结果正确的是( )
| A. | x3•x3=2x3 | B. | (-x3)2=-x6 | C. | (5x)3=125x3 | D. | x5÷x=x5 |
 如图,一个弯形管道ABCD得拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB、CD平行吗?写出完整推理说明理由.
如图,一个弯形管道ABCD得拐角∠ABC=115°,∠BCD=65°,这时管道所在的直线AB、CD平行吗?写出完整推理说明理由.