题目内容
4.观察下列各式:13=1=$\frac{1}{4}×{1^2}×{2^2}$;13+23=9=$\frac{1}{4}×{2^2}×{3^2}$;13+23+33=36=$\frac{1}{4}×{3^2}×{4^{{2^{\;}}}}$;13+23+33+43=100=$\frac{1}{4}×{4^2}×{5^2}$…回答下面的问题:
(1)13+23+33+43+…+103=$\frac{1}{4}$×102×112(写出算式即可);
(2)计算13+23+33+…+993+1003的值;
(3)计算:113+123+…+993+1003的值.
分析 (1)(2)由题意可知:从1开始连续自然数的立方和,等于最后一个自然数的平方乘这个自然数加1的平方的$\frac{1}{4}$,由此规律计算得出答案即可;
(3)由(2)的结果减去(1)的结果即可.
解答 解:(1)13+23+33+43+…+103=$\frac{1}{4}$×102×112;
(2)13+23+33+…+993+1003
=$\frac{1}{4}$×1002×1012
=25502500;
(3)$\frac{1}{4}$×1002×1012-$\frac{1}{4}$×102×112
=25502500-3025
=25499475.
点评 此题考查数字的变化规律,抓住数字特点,找出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
14.如果a是b的近似值,那么我们把b叫做a的真值,若用四舍五入法得到的近似数是75,则下列各数不可能是其真值的是( )
| A. | 75.01 | B. | 75.49 | C. | 74.99 | D. | 74.49 |
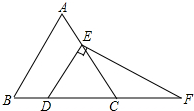 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.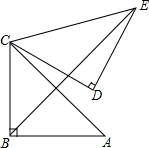 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.