题目内容
13.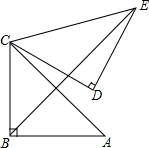 如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.
如图,在Rt△ABC中,∠ABC=90°,AB=BC=$\sqrt{2}$,将△ABC绕点C逆时针旋转60°,得到△CDE,连结BE,求BE的长.
分析 作BE交AC于H,如图,先利用勾股定理计算出AC=$\sqrt{2}$AB=2,再利用旋转的性质得CA=CE,∠ACE=60°,则可判断△ACE为等边三角形,所以EC=EA,加上BC=BA,于是可判断BE为AC的垂直平分线,根据根据等腰直角三角形的性质和等边三角形的性质得到BH=$\frac{1}{2}$AC=1,EH=$\frac{\sqrt{3}}{2}$AC=$\sqrt{3}$,从而可得到BE的长.
解答 解:作BE交AC于H,如图,
∵∠ABC=90°,AB=BC=$\sqrt{2}$,
∴AC=$\sqrt{2}$AB=2,
∵△ABC绕点C逆时针旋转60°得到△CDE,
∴CA=CE,∠ACE=60°,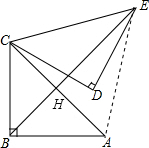
∴△ACE为等边三角形,
∴EC=EA,
∵BC=BA,
∴BE为AC的垂直平分线,
∴BH=$\frac{1}{2}$AC=1,EH=$\frac{\sqrt{3}}{2}$AC=$\sqrt{3}$,
∴BE=BH+EH=1+$\sqrt{3}$.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.本题的关键是证明BE垂直平分AC.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
3.一种面粉的质量标识为“30±0.2千克”,则下列面粉中合格的是( )
| A. | 29.2千克 | B. | 29.9千克 | C. | 30.5千克 | D. | 32.2千克 |
5.在△ABC中,A,B都是锐角,且sinA=$\frac{\sqrt{3}}{2}$,tanB=$\sqrt{3}$,AB=8,则AB边上的高为( )
| A. | 4$\sqrt{3}$ | B. | 8$\sqrt{3}$ | C. | 16$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
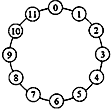 如图,圆圈内分别标有0,1,2,3,4,…,11这12个数字.电子跳蚤每跳一次,可以从一个圆圈跳到相邻的圆圈,现在,一只电子跳蚤从标有数字“0”的圆圈开始,按逆时针方向跳了2015次后,落在一个圆圈中,该圆圈所标的数字是1.
如图,圆圈内分别标有0,1,2,3,4,…,11这12个数字.电子跳蚤每跳一次,可以从一个圆圈跳到相邻的圆圈,现在,一只电子跳蚤从标有数字“0”的圆圈开始,按逆时针方向跳了2015次后,落在一个圆圈中,该圆圈所标的数字是1.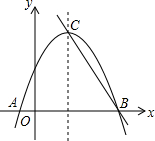 如图,抛物线y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$与x轴相交于A、B两点,抛物线的顶点为C,问:在抛物线的对称轴上是否存在一点P,使⊙P与x轴和直线BC都相切?若存在,请求出P的坐标;若不存在,请说明理由.
如图,抛物线y=-$\frac{4}{9}$x2+$\frac{16}{9}$x+$\frac{20}{9}$与x轴相交于A、B两点,抛物线的顶点为C,问:在抛物线的对称轴上是否存在一点P,使⊙P与x轴和直线BC都相切?若存在,请求出P的坐标;若不存在,请说明理由.