题目内容
已知a=
,求
+
的值.
| 1 | ||
|
a2+1+
| ||
a+1-
|
a+1-
| ||
a+1+
|
考点:二次根式的化简求值
专题:计算题
分析:先利用分母有理化得到a=
+1,再利用因式分解的方法化简原式得到
+
,然后分母有理化、合并后把a的值代入计算.
| 2 |
| ||||
|
| ||||
|
解答:解:∵a=
,
∴a=
+1,
原式=
+
=
+
=(
+
)2+(
-
)2,
=4a+2
=4(
+1)+2
=4
+6.
| 1 | ||
|
∴a=
| 2 |
原式=
| ||||||
|
| ||||||
|
=
| ||||
|
| ||||
|
=(
| a+1 |
| a |
| a+1 |
| a |
=4a+2
=4(
| 2 |
=4
| 2 |
点评:本题考查了二次根式的化简求值:二次根式的化简求值,一定要先化简再代入求值.二次根式运算的最后,注意结果要化到最简二次根式,二次根式的乘除运算要与加减运算区分,避免互相干扰.

练习册系列答案
相关题目
下列说法正确的是( )
| A、最小的整数是1 |
| B、最大的负数是-1 |
| C、最大的负整数是-1 |
| D、最小的有理数是0 |
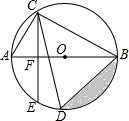 已知AB是⊙O的直径,AB=10cm,弦AC=6cm,弦CE⊥AB,垂足为F,弦CD平分∠ACB.
已知AB是⊙O的直径,AB=10cm,弦AC=6cm,弦CE⊥AB,垂足为F,弦CD平分∠ACB. 如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数.
如图,已知NG平分∠BNF,∠AMD=∠MNF,∠CMN:∠DMN=3:5,试求∠MNF和∠GNF的度数. 如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数.
如图,在△ABC中,AC=AB,AB的垂直平分线交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16,求△BCF的周长和∠EFC的度数.