题目内容
 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数;
(3)D为AB延长线上一点,点E在BC边所在射线上,且BE=BD=2AB,计算AE与CD所在直线的夹角,如果△ABC的面积是1,连接DE,计算△ADE的面积.
考点:全等三角形的判定与性质
专题:
分析:(1)直接运用HL定理证明即可解决问题.
(2)求出∠AEB=75°;证明∠BDC=∠AEB,即可解决问题.
(3)证明∠BDC=∠BEA,得到∠AFD=90°;由面积公式求出AB的长度,即可解决问题.
(2)求出∠AEB=75°;证明∠BDC=∠AEB,即可解决问题.
(3)证明∠BDC=∠BEA,得到∠AFD=90°;由面积公式求出AB的长度,即可解决问题.
解答: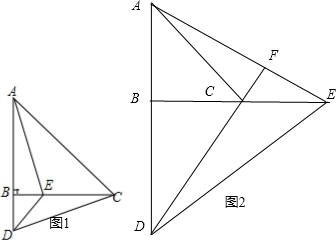 解:(1)如图1,
解:(1)如图1,
在直角△ABE与△CBD中,
,
∴△ABE≌△CBD(HL).
(2)∵AB=CB,∠ABC=90°,
∴∠ACB=45°,而∠EAC=30°,
∴∠AEB=45°+30°=75°;
∵△ABE≌△CBD,
∴∠BDC=∠AEB=75°.
(3)如图2,类似(1)中的方法,同理可证:△ABE≌△CBD,
∴∠BDC=∠BEA;
∵∠BEA+∠BAC=90°,
∴∠BDC+∠BEA=90°,
∴∠AFD=90°,
即AE与CD所在直线的夹角为90°;
∵
AB•BC=1,AB=BC,
∴AB=
,BE=BD=2
,
∴计算△ADE的面积=
×2
×
+
×2
×2
=2+4=6.
 解:(1)如图1,
解:(1)如图1,在直角△ABE与△CBD中,
|
∴△ABE≌△CBD(HL).
(2)∵AB=CB,∠ABC=90°,
∴∠ACB=45°,而∠EAC=30°,
∴∠AEB=45°+30°=75°;
∵△ABE≌△CBD,
∴∠BDC=∠AEB=75°.
(3)如图2,类似(1)中的方法,同理可证:△ABE≌△CBD,
∴∠BDC=∠BEA;
∵∠BEA+∠BAC=90°,
∴∠BDC+∠BEA=90°,
∴∠AFD=90°,
即AE与CD所在直线的夹角为90°;
∵
| 1 |
| 2 |
∴AB=
| 2 |
| 2 |
∴计算△ADE的面积=
| 1 |
| 2 |
| 2 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
点评:该题主要考查了全等三角形的判定及其性质的应用问题;牢固掌握定理内容是灵活运用、解题的基础和关键.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
 如图,在四边形ABCD中,AD∥BC,AB=BC=3BE,CE=
如图,在四边形ABCD中,AD∥BC,AB=BC=3BE,CE= 按照下列要求完成作图及相应的问题解答
按照下列要求完成作图及相应的问题解答
 易拉罐的形状是圆柱,其底面的直径为6cm,将10个相同的易拉罐按如图方式堆放,则这10个易拉罐所达到的最大高度是
易拉罐的形状是圆柱,其底面的直径为6cm,将10个相同的易拉罐按如图方式堆放,则这10个易拉罐所达到的最大高度是