题目内容
4.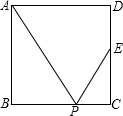 如图,在正方形ABCD中,如果E为CD边的中点,P是BC边上的一动点,那么下列条件中,能推出△ABP与△ECP相似的是( )
如图,在正方形ABCD中,如果E为CD边的中点,P是BC边上的一动点,那么下列条件中,能推出△ABP与△ECP相似的是( )| A. | BP:BC=1:3 | B. | BP:BC=1:2 | C. | BP:BC=2:3 | D. | BP:BC=3:4 |
分析 若要证△ABP∽△ECP,只需证出$\frac{AB}{EC}$=$\frac{BP}{CP}$,由点E为CD边的中点结合正方形的性质可得出BP=2CP,进而即可得出BP与BC直接的比例关系,此题得解.
解答 解:若证△ABP∽△ECP,只需证出$\frac{AB}{EC}$=$\frac{BP}{CP}$,
∵E为CD边的中点,四边形ABCD为正方形,
∴BP=2CP,
∴BP:BC=2CP:(2CP+CP)=2:3.
故选C.
点评 本题考查了相似三角形的判定与正方形的性质,牢记“两组对应边的比相等且夹角对应相等的两个三角形相似”是解题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
17.一个等腰三角形的两边分别为2,3,则这个三角形的周长为( )
| A. | 3+4 | B. | 6+2 | C. | 6+4 | D. | 3+4或6+2 |
18.如图,若有一个几何体的三视图如图所示,则这个几何体是( )


| A. | 三棱柱 | B. | 四棱柱 | C. | 五棱柱 | D. | 长方体 |
14.单项式-$\frac{5xy}{3}$的系数和次数分别是( )
| A. | -$\frac{1}{3}$,1 | B. | -$\frac{5}{3}$,1 | C. | $\frac{5}{3}$,2 | D. | -$\frac{5}{3}$,2 |
19.下列各组线段中,成比例线段的组是( )
| A. | 3cm,4cm,5cm,8cm | B. | 1cm,3cm,4cm,8cm | C. | 2cm,3cm,4cm,6cm | D. | 2cm,6cm,4cm,8cm |
9.正方形具有而矩形不一定具有的性质是( )
| A. | 对角线相等 | B. | 对角线互相平分 | ||
| C. | 对角线互相垂直 | D. | 对角线互相平分且相等 |
16.下列四个数中,最小的数是( )
| A. | -$\frac{1}{3}$ | B. | -3 | C. | 0 | D. | $\frac{1}{3}$ |
13.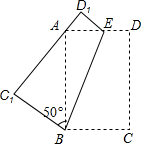 如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
 如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
14.若$\frac{1}{3}$a2n+1b2与5a3n-2b2是同类项,则n=( )
| A. | $\frac{3}{5}$ | B. | -3 | C. | -$\frac{5}{3}$ | D. | 3 |