题目内容
1.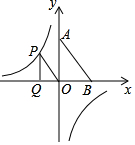 在平面直角坐标系中,A(0,2),B(1,0),点P是反比例函数y=-$\frac{1}{x}$上的一个动点,过点P作PQ⊥x轴,垂足为Q,若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P有( )个.
在平面直角坐标系中,A(0,2),B(1,0),点P是反比例函数y=-$\frac{1}{x}$上的一个动点,过点P作PQ⊥x轴,垂足为Q,若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P有( )个.| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 设点P的坐标为(m,-$\frac{1}{m}$),根据相似三角形的性质可得出关于m的方程,解之即可得出得出m的值,进而即可得出符合题意的点P的个数.
解答 解:设点P的坐标为(m,-$\frac{1}{m}$),
∵以点O、P、Q为顶点的三角形与△OAB相似,
∴$\frac{OQ}{OB}$=$\frac{PQ}{OA}$或$\frac{OQ}{OA}$=$\frac{PQ}{OB}$,
即$\frac{|m|}{1}$=$\frac{1}{|2m|}$或$\frac{|m|}{2}$=$\frac{1}{|m|}$,
解得:m=±$\frac{\sqrt{2}}{2}$或m=±$\sqrt{2}$,
∴符合题意得点P有4个.
故选D.
点评 本题考查了反比例函数图象上点的坐标特征以及相似三角形的性质,牢记“两组对应边的比相等且夹角对应相等的两个三角形相似”是解题的关键.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
13.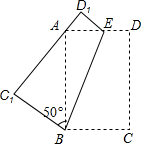 如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
 如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )
如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D两点分别落在点C1、D1处.若∠C1BA=50°,则∠ABE的度数为( )| A. | 10° | B. | 20° | C. | 30° | D. | 40° |
14.若$\frac{1}{3}$a2n+1b2与5a3n-2b2是同类项,则n=( )
| A. | $\frac{3}{5}$ | B. | -3 | C. | -$\frac{5}{3}$ | D. | 3 |
5.下列图形具有稳定性的是( )
| A. | 正五边形 | B. | 三角形 | C. | 梯形 | D. | 正方形 |
3.$\frac{4}{9}$的分子加上8,要使原分数大小不变,分母应加上( )
| A. | 8 | B. | 18 | C. | 27 | D. | 36 |




 B.
B.  C.
C.  D.
D. 