题目内容
某仓库有50件同一规格的某种集装箱,准备委托运输公司送到码头,运输公司提供如下运输信息表:
由于时间紧急,要求一次运完,运输公司按客户要求安排20辆货车刚好一次运完,问这三种型号的货车各需多少辆,有多少种安排方式?哪种安排方式所需运费最少?最少运费是多少?
| 运输车型号 | A | B | C |
| 每次运输集装箱(件) | 1 | 2 | 3 |
| 每次运费(元) | 120 | 160 | 180 |
考点:三元一次不定方程
专题:
分析:先设需要装运1件、2件、3件集装箱的货车分别为x辆、y辆、z辆,再根据题意列出关于x、y、z的方程组,用x表示出y、z的值,再根据y≥0即可求出符合条件的未知数的对应值.
解答:解:设需要装运1件、2件、3件集装箱的货车分别为x辆、y辆、z辆,根据题意得
,
①×3-②得2x+y=10,
则
,
因为y≥0,
所以0≤x≤5,
故x只能取0、1、2、3、4、5,
共有
、
、
、
、
、
,这六种安排方法:
设总运费为F元,则F=120x+160y+180z=120x+160(10-2x)+180(10+x),
所以F=3400-20x,
当x=5时,总运费最低,最低运费为F=3400-20×5=3300元.
|
①×3-②得2x+y=10,
则
|
因为y≥0,
所以0≤x≤5,
故x只能取0、1、2、3、4、5,
共有
|
|
|
|
|
|
设总运费为F元,则F=120x+160y+180z=120x+160(10-2x)+180(10+x),
所以F=3400-20x,
当x=5时,总运费最低,最低运费为F=3400-20×5=3300元.
点评:本题考查的是三元一次不定方程的应用,根据题意列出三元一次不定方程是解答此题的关键.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
 如图,四边形ABCD的两条对角线相交于点O,AO=CO,BO=DO.求证:AB∥CD.
如图,四边形ABCD的两条对角线相交于点O,AO=CO,BO=DO.求证:AB∥CD.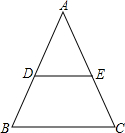 在△ABC中,点D是AB边的中点,且DE∥BC,则S△ADE:S梯形DBCE=
在△ABC中,点D是AB边的中点,且DE∥BC,则S△ADE:S梯形DBCE=