题目内容
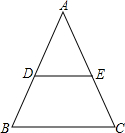在△ABC中，点D是AB边的中点，且DE∥BC，则S△ADE：S梯形DBCE=考点：相似三角形的判定与性质
专题：
分析：由DE∥BC，D为中点可知
=
，且△ADE∽△ABC，利用相似三角形的性质可知S△ADE=
S△ABC，进一步可求得答案．
| AD |
| AB |
| 1 |
| 2 |
| 1 |
| 4 |
解答：解：∵DE∥BC，
∴
=
，且△ADE∽△ABC，
∴
=
，
∴S△ADE=
S△ABC，S梯形DBCE=
S△ABC，
∴S△ADE：S梯形DBCE=1：3，
故答案为：1：3．
∴
| AD |
| AB |
| 1 |
| 2 |
∴
| S△ADE |
| S△ABC |
| 1 |
| 4 |
∴S△ADE=
| 1 |
| 4 |
| 3 |
| 4 |
∴S△ADE：S梯形DBCE=1：3，
故答案为：1：3．
点评：本题主要考查三角形相似的判定和性质，由条件得到△ADE∽△ABC，且相似比为1：2是解题的关键．
练习册系列答案
相关题目
数a、b在数轴上的位置如图所示，化简a-|b-a|=