题目内容
点A、B、C在同一直线上,M、N分别是线段AC、BC的中点.
(1)AC=10,BC=6,求MN;
(2)AB=16,求MN;
(3)AB=m,求MN;
(4)探究AB与MN的关系;
(5)若A、B、C不共线,猜想AB与MN的关系.
(1)AC=10,BC=6,求MN;
(2)AB=16,求MN;
(3)AB=m,求MN;
(4)探究AB与MN的关系;
(5)若A、B、C不共线,猜想AB与MN的关系.
考点:两点间的距离
专题:
分析:(1)根据线段中点的定义可得CM=
AC,BN=
CN,再分点C在线段AB上和点B在线段AC上两种情况分别求解即可;
(2)(3)根据(1)的结论分别求解即可;
(4)根据(3)的结论解答;
(5)根据三角形的中位线平行于第三边并且等于第三边的一半解答.
| 1 |
| 2 |
| 1 |
| 2 |
(2)(3)根据(1)的结论分别求解即可;
(4)根据(3)的结论解答;
(5)根据三角形的中位线平行于第三边并且等于第三边的一半解答.
解答: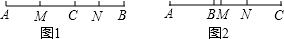 解:(1)∵M、N分别是线段AC、BC的中点,
解:(1)∵M、N分别是线段AC、BC的中点,
∴CM=
AC=
×10=5,BN=
BC=
×6=3,
如图1,点C在线段AB上时,MN=CM+CN=5+3=8,
如图2,点B在线段AC上时,MN=CM-CN=5-3=2;
(2)AB=16时,MN=
×16=8;
(3)AB=m时,MN=
AB=
m;
(4)MN=
AB;
(5)若A、B、C不共线时,AB=
MN.
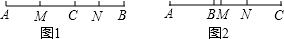 解:(1)∵M、N分别是线段AC、BC的中点,
解:(1)∵M、N分别是线段AC、BC的中点,∴CM=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
如图1,点C在线段AB上时,MN=CM+CN=5+3=8,
如图2,点B在线段AC上时,MN=CM-CN=5-3=2;
(2)AB=16时,MN=
| 1 |
| 2 |
(3)AB=m时,MN=
| 1 |
| 2 |
| 1 |
| 2 |
(4)MN=
| 1 |
| 2 |
(5)若A、B、C不共线时,AB=
| 1 |
| 2 |
点评:本题考查了两点间的距离,主要利用了线段中点的定义,难点在于分情况讨论,作出图形更形象直观.

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
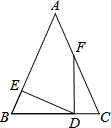 如图,已知△ABC中,点D为BC上一点,E、F两点分别在边AB、AC上,若BE=CD,BD=CF,∠B=∠C,∠A=50°,则∠EDF=
如图,已知△ABC中,点D为BC上一点,E、F两点分别在边AB、AC上,若BE=CD,BD=CF,∠B=∠C,∠A=50°,则∠EDF= 数a、b在数轴上的位置如图所示,化简a-|b-a|=
数a、b在数轴上的位置如图所示,化简a-|b-a|=