题目内容
11.已知|a|=5,|b|=2,且|a+b|≠a+b,求a3+b2-ab的值.分析 先由绝对值的性质求得a、b的值,然后根据|a+b|≠a+b可得到a=5,b=-2或a=-5,b=-2或a=-5,b=2,最后代入计算即可.
解答 解:∵|a|=5,|b|=2,
∴a=±5,b=±2.
∵|a+b|≠a+b,
∴a=5,b=-2或a=-5,b=-2或a=-5,b=2.
当a=5,b=-2时,a3+b2-ab=53+(-2)2-5×(-2)=125+4+10=139;
当a=-5,b=-2时a3+b2-ab=(-5)3+(-2)2-(-5)×(-2)=-125+4-10=-131;
当a=-5,b=2时a3+b2-ab=(-5)3+22-(-5)×2=-125+4+10=-111.
综上所述,代数式的值为139或-131或-111.
点评 本题主要考查的是求代数式的值、绝对值的定义和性质,求得a=5,b=-2或a=-5,b=-2或a=-5,b=2是解题的关键.

练习册系列答案
相关题目
16.矩形两对角线交角为60°,且一条对角线与最短边的和为10,则对角线的长是( )
| A. | $\frac{10}{3}$ | B. | $\frac{20}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{25}{3}$ |
 如图.已知:AB=6cm,BC=$\frac{1}{2}$AB,D为AC的中点,求DB的长.
如图.已知:AB=6cm,BC=$\frac{1}{2}$AB,D为AC的中点,求DB的长.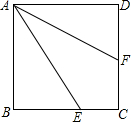 如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.
如图,已知正方形ABCD,点E在BC上,BE=2EC,点F在CD上,∠EAF=30°,求$\frac{CF}{DF}$.