题目内容
19.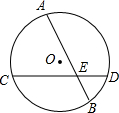 如图,点A、C、B、D在⊙O上,且$\widehat{AB}=\widehat{CD}$,弦AB、CD相交于点E,AE与CE相等吗?为什么?
如图,点A、C、B、D在⊙O上,且$\widehat{AB}=\widehat{CD}$,弦AB、CD相交于点E,AE与CE相等吗?为什么?
分析 连接AC,由已知条件得出$\widehat{AD}=\widehat{CB}$,由圆周角定理得出∠C=∠A,即可得出结论.
解答 解:AE=CE;理由如下:
连接AC,如图所示:
∵$\widehat{AB}=\widehat{CD}$,
∴$\widehat{AD}=\widehat{CB}$,
∴∠C=∠A,
∴AE=CE.
点评 本题考查了圆心角、弧、弦的关系定理、圆周角定理、等腰三角形的判定方法;熟练掌握圆周角定理,由题意得出弧相等是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.一个三位数,各个数位上数字之和为10,百位数字比十位数字大1.如果百位数字与个位数字对调,则所得新数比原数的3倍还大61,那么原来的三位数是( )
| A. | 235 | B. | 216 | C. | 217 | D. | 208 |
7. 如图,△ABC内接于⊙O,∠BOC=80°,则∠BAC的度数为( )
如图,△ABC内接于⊙O,∠BOC=80°,则∠BAC的度数为( )
 如图,△ABC内接于⊙O,∠BOC=80°,则∠BAC的度数为( )
如图,△ABC内接于⊙O,∠BOC=80°,则∠BAC的度数为( )| A. | 120° | B. | 160° | C. | 40° | D. | 10° |
4.在下列各数中,其中无理数的是( )
| A. | $\frac{7}{22}$ | B. | 0.303003 | C. | -3.14159 | D. | 2π |
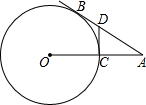 如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,点D在AB上,且DB=DC.
如图,AB是⊙O的切线,切点为B,AO交⊙O于点C,点D在AB上,且DB=DC.