题目内容
 如图,△ABC中,∠ACB=90°,∠A=30°,AC的中垂线交AC于E.交AB于D,则图中60°的角共有( )
如图,△ABC中,∠ACB=90°,∠A=30°,AC的中垂线交AC于E.交AB于D,则图中60°的角共有( )| A、6个 | B、5个 | C、4个 | D、3个 |
考点:线段垂直平分线的性质
专题:
分析:由线段垂直平分线的性质可求得∠A=∠ACD=30°,可求得∠ADE=∠CDE=60°,结合直角三角形的性质可求得∠B=∠BCD=∠BDC=60°,可求得答案.
解答:解:
∵DE为线段AC的垂直平分线,
∴DC=DA,
∴∠A=∠ACD=30°,
∵∠ACB=90°,DE⊥AC,
∴∠DCB=∠ADE=∠CDE=60°,
又∠A+∠B=90°,
∴∠B=60°,
∴△BCD为等边三角形,
∴∠CDB=60°,
∴在图中为60°的角有5个,
故选B.
∵DE为线段AC的垂直平分线,
∴DC=DA,
∴∠A=∠ACD=30°,
∵∠ACB=90°,DE⊥AC,
∴∠DCB=∠ADE=∠CDE=60°,
又∠A+∠B=90°,
∴∠B=60°,
∴△BCD为等边三角形,
∴∠CDB=60°,
∴在图中为60°的角有5个,
故选B.
点评:本题主要考查线段垂直平分线的性质,掌握线段垂直平分线上的点到线段两端点的距离相等是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
若x>y,则下列式子正确的是( )
| A、x-5>y+5 |
| B、5x>5y |
| C、-5x+3>-5y+3 |
| D、ax>ay |
 从正面观察下图所示的两个几何体,你看到的是( )
从正面观察下图所示的两个几何体,你看到的是( )A、 |
B、 |
C、 |
D、 |
下列长度的各种线段,可以组成三角形的是( )
| A、1,2,3 |
| B、1,5,5 |
| C、3,3,6 |
| D、1,5,6 |
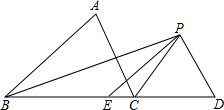 已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长.
已知,如图,△ABC中,BC=10,CD=6,BP平分∠ABC,CP平分∠ACD,PD∥AC,PE∥AB,求△PED的周长. 如图,将1、2、3…这些正整数依次填入图中的方格内,任意从一纵列用阴影框出4个小方格,其中这4个小方格中的第三个小方格的数是n,则这4个小方格内的4个数的和为
如图,将1、2、3…这些正整数依次填入图中的方格内,任意从一纵列用阴影框出4个小方格,其中这4个小方格中的第三个小方格的数是n,则这4个小方格内的4个数的和为 已知,如图∠1=∠2,∠A=∠F,请问∠C=∠D相等吗?试写出推理过程.
已知,如图∠1=∠2,∠A=∠F,请问∠C=∠D相等吗?试写出推理过程.