题目内容
2.如图,△ABC和△DBC都是等边三角形,点B1在BC上,沿BC方向将△DBC平移到△D1B1C1的位置.此时,四边形ABD1C1是平行四边形吗?证明你的结论.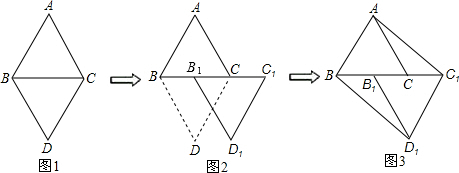
分析 先根据等边三角形的性质得AB=BC=CD,∠ABC=∠DCB=60°,再根据平移的性质得CD=C1D1,∠DCB=∠D1C1B1=60°,则AB=C1D1,∠ABC=∠D1C1B1,根据平行线的判定得AB∥C1D1,然后根据平行四边形的判定方法得四边形ABD1C1是平行四边形.
解答 解:四边形ABD1C1是平行四边形.理由如下:
∵△ABC和△DBC都是等边三角形,
∴AB=BC=CD,∠ABC=∠DCB=60°,
∵沿BC方向将△DBC平移得到△D1B1C1,
∴CD=C1D1,∠DCB=∠D1C1B1=60°,
∴AB=C1D1,∠ABC=∠D1C1B1,
∴AB∥C1D1,
∴四边形ABD1C1是平行四边形.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同;新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了等边三角形的性质和平行四边形的判定.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
10.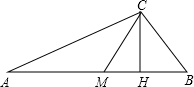 如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
 如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )| A. | AB2=AC2+BC2 | B. | CH2=AH•HB | C. | CM=$\frac{1}{2}$AB | D. | CB=$\frac{1}{2}$AB |
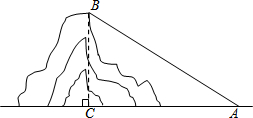 如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,求山的高度BC.(精确到0.1米)
如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,求山的高度BC.(精确到0.1米)
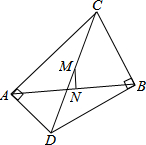 如图,∠CAD和∠CBD都是直角,M是CD的中点,N是AB的中点.求证:直线MN是AB的垂直平分线.
如图,∠CAD和∠CBD都是直角,M是CD的中点,N是AB的中点.求证:直线MN是AB的垂直平分线. 如图,5个正方形重叠,重叠部分的顶点正好是下面一个正方形的中心.若每个正方形的边长都是a,则整个图形的周长是12a.
如图,5个正方形重叠,重叠部分的顶点正好是下面一个正方形的中心.若每个正方形的边长都是a,则整个图形的周长是12a.