题目内容
7. 如图,在四边形ABCD中,∠A=90°,AD=8.对角线BD⊥CD,P是BC边上一动点,连结PD.若∠ADB=∠C,则PD长的最小值为8.
如图,在四边形ABCD中,∠A=90°,AD=8.对角线BD⊥CD,P是BC边上一动点,连结PD.若∠ADB=∠C,则PD长的最小值为8.
分析 根据垂线段最短,当DP垂直于BC的时候,DP的长度最小.结合已知条件,利用三角形的内角和定理推出∠ABD=∠CBD,由角平分线性质即可得AD=DP,由AD的长可得DP的长.
解答 解:根据垂线段最短,当DP⊥BC的时候,DP的长度最小.
∵BD⊥CD,即∠BDC=90°,又∠A=90°,
∴∠A=∠BDC,又∠ADB=∠C,
∴∠ABD=∠CBD,又DA⊥BA,BD⊥DC,
∴AD=DP,又AD=8,
∴DP=8.
故答案为:8.
点评 本题考查了角平分线上的点到角的两边距离相等的性质,垂线段最短的性质,熟记性质并判断出DP最小时的位置是解题的关键.

练习册系列答案
相关题目
17.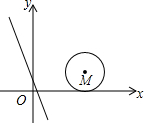 如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )
如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )
 如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )
如图,在平面直角坐标系中,半径为2的⊙M的圆心坐标是(4,2),将直线y=-2x+1向上平移k个单位后恰好与⊙M相切,则k的值是( )| A. | 1+$\sqrt{5}$或1+2$\sqrt{5}$ | B. | 1+2$\sqrt{5}$或1+4$\sqrt{5}$ | C. | 9+2$\sqrt{5}$或9-2$\sqrt{5}$ | D. | 10+2$\sqrt{5}$或10-2$\sqrt{5}$ |
18. 如图所示,若a∥b,∠1=120°,则∠2=( )
如图所示,若a∥b,∠1=120°,则∠2=( )
 如图所示,若a∥b,∠1=120°,则∠2=( )
如图所示,若a∥b,∠1=120°,则∠2=( )| A. | 55° | B. | 60° | C. | 65° | D. | 75° |
2.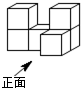 如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
 如图是由6个完全相同的小正方体组成的几何体,其左视图为( )
如图是由6个完全相同的小正方体组成的几何体,其左视图为( )| A. | 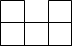 | B. | 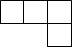 | C. | 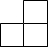 | D. | 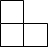 |
 如图,已知AB∥CD,CE平分∠ACD,当∠A=120°时,∠ECD的度数是30°.
如图,已知AB∥CD,CE平分∠ACD,当∠A=120°时,∠ECD的度数是30°.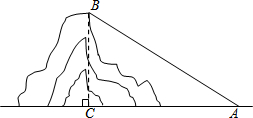 如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,求山的高度BC.(精确到0.1米)
如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,求山的高度BC.(精确到0.1米)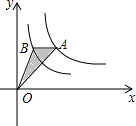 如图,点A和点B在第一象限,A是双曲线y=$\frac{3}{x}$上的一点,B是双曲线y=$\frac{1}{x}$上的一点,且AB平行于x轴,连接OA,OB,则△AOB的面积为1.
如图,点A和点B在第一象限,A是双曲线y=$\frac{3}{x}$上的一点,B是双曲线y=$\frac{1}{x}$上的一点,且AB平行于x轴,连接OA,OB,则△AOB的面积为1.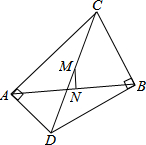 如图,∠CAD和∠CBD都是直角,M是CD的中点,N是AB的中点.求证:直线MN是AB的垂直平分线.
如图,∠CAD和∠CBD都是直角,M是CD的中点,N是AB的中点.求证:直线MN是AB的垂直平分线.