题目内容
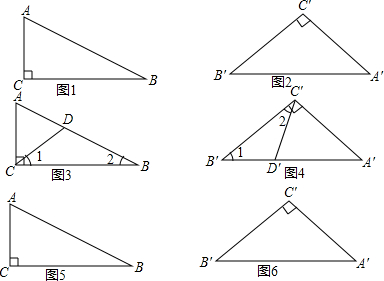
5.如图1和图2,在△ABC和△A′B′C′,其中∠C=∠C′=90°,且两个三角形不相似.问:能否分别用一条直线分割这两个三角形,使△ABC所分割成的两个三角形与△A′B′C′所分割成的两个三角形分别对应相似?如果能,请设计出分割方案;如果不能,请说明理由.问题解决
小华通过分割∠C和∠C′,解决了问题,示意图3和图4如下(图中∠DCB=∠B′;∠D′C′B′=∠B:)
小阳说:不分割∠C和∠C′,也能解决问题.请你尝试根据小阳的解决思路解决问题.(在所给图形(图5和图6)上画出分割线,并注明相等的角即可)
结论推广
小冯发现:对于有一个角相等的两个不相似的三角形,一定可以把每一个三角形分割成两个小三角形,使分割的两个小三角形分别对应相似.请对他的发现作出解释.
深入研究
小鹏还发现:对于三角都不相等的两个三角形,不可以把每一个三角形分割成两个小三角形,使分割出的小三角形分别对应相似.
请你继续探索,对于三角都不相等的两个三角形,可以把三角形分割成三个小三角形,使分割出的小三角形分别对应相似吗?如果可以,请设计出分割方案(画出示意图或说明操作步骤);如果不可以,请说明理由.
分析 问题解决:如图a,不妨设∠CAB>∠A′,∠C′B′A′>∠B.可将∠CAB分成两部分,使得其中一部分∠DAB=∠A′,将∠C′B′A′分成两部分,使得其中一部分∠D′B′A′=∠B,根据两角对应相等的两个三角形相似可得△ADB∽△A′D′B′.由∠ADC=∠1+∠B=∠A′+∠2=∠B′D′C′,∠C=∠C′,可得△ACD∽△B′C′D′;
结论推广:如图b,与“问题解决”中的方法一样,不妨设∠CAB>∠A′,∠C′B′A′>∠B.作∠DAB=∠A′,作∠D′B′A′=∠B,即可得到△ADB∽△A′D′B′.易证∠ADC=∠B′D′C′,又因为∠C=∠C′,所以△ACD∽△B′C′D′;
深入研究:如图c,不妨设∠CAB>∠A′,∠C′B′A′>∠B.作∠DAB=∠A′,作∠D′B′A′=∠B,即可得到△ADB∽△A′D′B′.不妨设∠ACD>∠C′B′D′,∠B′C′D′>∠CAD,同样作∠ACE=∠C′B′D′(即∠3=∠4),作∠E′C′B′=∠EAC(即∠6=∠5),即可得到△ACE∽△C′B′E′.又因为∠EDC=∠1+∠B=∠A′+∠2=∠E′D′C′,∠CED=∠3+∠5=∠4+∠6=∠C′E′D′,即可得到△CED∽△C′E′D′.
解答 解:问题解决
如图a,∠C=∠C′=90°,不妨设∠CAB>∠A′,∠C′B′A′>∠B.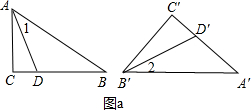
作∠DAB=∠A′(即∠1=∠A′),作∠D′B′A′=∠B(即∠2=∠B),
则有△ADB∽△A′D′B′.
∵∠ADC=∠1+∠B=∠A′+∠2=∠B′D′C′,∠C=∠C′,
∴△ACD∽△B′C′D′;
结论推广
如图b,∠C=∠C′≠90°,不妨设∠CAB>∠A′,∠C′B′A′>∠B.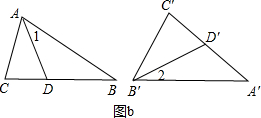
作∠DAB=∠A′(即∠1=∠A′),作∠D′B′A′=∠B(即∠2=∠B),
即可得到△ADB∽△A′D′B′.
∵∠ADC=∠1+∠B=∠A′+∠2=∠B′D′C′,∠C=∠C′,
∴△ACD∽△B′C′D′;
深入研究
如图c,不妨设∠CAB>∠A′,∠C′B′A′>∠B.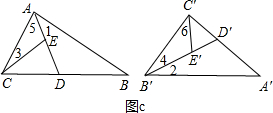
作∠DAB=∠A′(即∠1=∠A′),作∠D′B′A′=∠B(即∠2=∠B),
即可得到△ADB∽△A′D′B′.
不妨设∠ACD>∠C′B′D′,∠B′C′D′>∠CAD,
作∠ACE=∠C′B′D′(即∠3=∠4),作∠E′C′B′=∠EAC(即∠6=∠5),
即可得到△ACE∽△C′B′E′.
又因为∠EDC=∠1+∠B=∠A′+∠2=∠E′D′C′,∠CED=∠3+∠5=∠4+∠6=∠C′E′D′,
即可得到△CED∽△C′E′D′.
点评 本题是一道作图题,考查了相似三角形的判定、三角形的外角性质等知识,是一道以能力立意的好题,运用转化思想(将三角都不相等的两个三角形转化为有一个角相等的两个三角形)是解决本题的关键.

| A. | 买两件等值的商品可减100元,再打3折,最后不到1000元 | |
| B. | 买两件等值的商品可减100元,再打7折,最后不到1000元 | |
| C. | 买两件等值的商品可打3折,再减100元,最后不到1000元 | |
| D. | 买两件等值的商品可打7折,再减100元,最后不到1000元 |
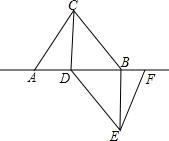 △ABC和△DEF都是边长为6cm的等边三角形,且A、D、B、F在同一直线上,连接CD、BF.
△ABC和△DEF都是边长为6cm的等边三角形,且A、D、B、F在同一直线上,连接CD、BF.