题目内容
11.已知,AB为⊙O的直径,C,D为⊙O上两点,过点D的直线EF与⊙O相切,分别交BA,BC的延长线于点E,F,BF⊥EF(I)如图①,若∠ABC=50°,求∠DBC的大小;
(Ⅱ)如图②,若BC=2,AB=4,求DE的长.
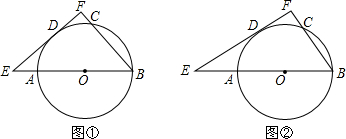
分析 (1)如图1,连接OD,BD,由EF与⊙O相切,得到OD⊥EF,由于BF⊥EF,得到OD∥BF,得到∠AOD=∠B=50°,由外角的性质得到结果;
(2)如图2,连接AC,OD,根据AB为⊙O的直径,得出∠ACB=90°,由直角三角形的性质得到∠CAB=30°,于是AC=AB•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,AH=AO•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,根据三角形的中位线的性质解得结果.
解答 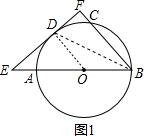 解(1)如图1,连接OD,BD,
解(1)如图1,连接OD,BD,
∵EF与⊙O相切,
∴OD⊥EF,
∵BF⊥EF,
∴OD∥BF,
∴∠AOD=∠B=50°,
∵OD=OB,
∴∠OBD=∠ODB=$\frac{1}{2}$∠AOD=25°;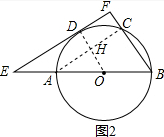
(2)如图2,连接AC,OD,
∵AB为⊙O的直径,
∴∠ACB=90°,
∵BC=2,AB=4,
∴∠CAB=30°,
∴AC=AB•cos30°=4×$\frac{\sqrt{3}}{2}$=2$\sqrt{3}$,
∵∠ODF=∠F=∠HCO=90°,
∴∠DHC=90°,
∴AH=AO•cos30°=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∵∠HAO=30°,
∴OH=$\frac{1}{2}$OA=$\frac{1}{2}$OD,
∵AC∥EF,
∴DE=2AH=2$\sqrt{3}$.
点评 本题考查了切线的性质,垂径定理,锐角三角函数,平行线的性质和判定,辅助线的作法是解题的关键.

练习册系列答案
相关题目
2.下面四个图形是多面体的展开图,其中不是棱柱的展开图的是( )
| A. | 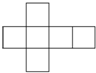 | B. | 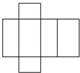 | C. | 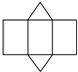 | D. | 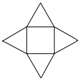 |
6.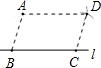 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
 如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )
如图,点A是直线l外一点,在l上取两点B,C,分别以A,C为圆心,BC,AB长为半径画弧,两弧交于点D,分别连接AB、AD、CD,则四边形ABCD一定是( )| A. | 平行四边形 | B. | 矩形 | C. | 菱形 | D. | 正方形 |
16.零上13℃记作+13℃,零下2℃记作( )
| A. | 2℃ | B. | -2℃ | C. | 2 | D. | -2 |
20.(-2)+3的值等于( )
| A. | -5 | B. | -1 | C. | -6 | D. | 1 |
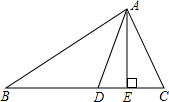 如图,AE、AD分别是△ABC的高和角平分线,且∠B=36°,∠C=66°,求∠DAE的度数.
如图,AE、AD分别是△ABC的高和角平分线,且∠B=36°,∠C=66°,求∠DAE的度数. 已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.
已知,如图AB=AC,CD⊥AB于D,BE⊥AC于E,BE和CD相交于点O,求证:AO平分∠BAC.