Question

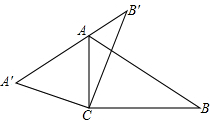在图中，△ABC为直角三角形，∠ACB=90°，∠B=30°，以点C为旋转中心，将△ABC旋转到△A′B′C′的位置，使A′B′经过点A．
（1）求∠ACA′的度数；
（2）求线段AC与线段A′B′的数量关系．

Answer 1

考点：旋转的性质

专题：

分析：（1）证明∠BAC=60°；证明AC=A′C，得到∠A′=∠A′AC=60°，求出∠ACA′=60°．
（2）由△ABC≌△A′B′C′，得到A′B′=AB；由（1）知AB=2AC，故A′B′=2AC．

解答：解：（1）如图，∵∠ACB=90°，∠B=30°，
∴AB=2AC，∠BAC=60°；
∵△ABC≌△A′B′C′，
∴∠A′=∠BAC=60°，AC=A′C，
∴∠A′=∠A′AC=60°，
∴∠ACA′=180°-120°=60°．
（2）∵△ABC≌△A′B′C′，
∴A′B′=AB；由（1）知：AB=2AC，
∴A′B′=2AC．

点评：该题主要考查了旋转变换的性质、等腰三角形的性质及其应用问题；解题的关键是灵活运用旋转变换的性质、等腰三角形的性质等来分析、判断、解答．