题目内容
如图，点B是线段AC上一点，且AC=12，BC=4．（1）求线段AB的长；
（2）如果点O是线段AC的中点，求线段OB的长．
考点：两点间的距离
专题：
分析：（1）根据线段的和差，可得答案；
（2）根据线段中点的性质，可得OC的长，再根据线段的和差，可得答案．
（2）根据线段中点的性质，可得OC的长，再根据线段的和差，可得答案．
解答：解：（1）由线段的和差，得
AB=AC-BC=12-4=8；
（2）由点O是线段AC的中点，得OC=
AC=
×12=6，
由线段的和差，得
OB=OC-BC=6-4=2．
AB=AC-BC=12-4=8；
（2）由点O是线段AC的中点，得OC=
| 1 |
| 2 |
| 1 |
| 2 |
由线段的和差，得
OB=OC-BC=6-4=2．
点评：本题考查了两点间的距离，利用了线段中点的性质，线段的和差．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知：如图，线段MN=m，延长MN到点C，使NC=n，点A为MC的中点，点B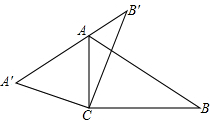
在图中，△ABC为直角三角形，∠ACB=90°，∠B=30°，以点C为旋转中心，将△ABC旋转到△A′B′C′的位置，使A′B′经过点A．正方形的边长为4，则其外接圆半径的长是（ ）
A、4
| ||
B、2
| ||
| C、2 | ||
D、
|
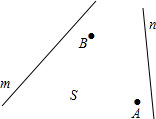如图，某公司要在公路m，n之间的S区域修建一所物流中心P．按照设计要求，物流中心P到区域S内的两个社区A、B的距离必须相等，到两条公路m、n的距离也必须相等．那么物流中心P应建在什么位置才符合设计要求？请你在图中画出它的位置并标出所求．（保留画图痕迹）
如图，四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”，如果大正方形面积为169，且直角三角形中较短的直角边的长为5，则中间小正方形面积（阴影部分）为