题目内容
两河流交汇于点M处，甲河流水速为4km/h，乙河流水速为2km/h，一船只在静水中的速度为10km/h．某次该船只，从甲河流的上游A行驶到交汇处M后再沿乙河流逆流而上到点B，总共行驶了69km．原路返回后，发现往返所用时间相等．求此次航行往返总时间．
考点：一元一次方程的应用
专题：
分析：可设甲河流的上游A到交汇处M的路程为xkm，则交汇处M到乙河流的路程为（69-x）km，根据时间的等量关系：原路返回后，发现往返所用时间相等，路程方程求解即可．
解答：解：设甲河流的上游A到交汇处M的路程为xkm，则交汇处M到乙河流的路程为（69-x）km，
依题意有
+
=
+
，
解得x=21，
（
+
）×2=（
+
）×2=15．
答：此次航行往返总时间是15h．
依题意有
| x |
| 10+4 |
| 69-x |
| 10-2 |
| 69-x |
| 10+2 |
| x |
| 10-4 |
解得x=21，
（
| x |
| 10+4 |
| 69-x |
| 10-2 |
| 21 |
| 14 |
| 69-21 |
| 8 |
答：此次航行往返总时间是15h．
点评：考查了一元一次方程的应用，解题关键是要读懂题目的意思，根据题目给出的条件，找出合适的等量关系列出方程，再求解．
练习册系列答案
科学实验活动册系列答案
相关题目
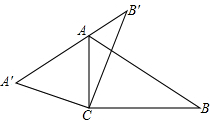在图中，△ABC为直角三角形，∠ACB=90°，∠B=30°，以点C为旋转中心，将△ABC旋转到△A′B′C′的位置，使A′B′经过点A．
如图，四个全等的直角三角形围成一个大正方形，中间空出的部分是一个小正方形，这样就组成了一个“赵爽弦图”，如果大正方形面积为169，且直角三角形中较短的直角边的长为5，则中间小正方形面积（阴影部分）为
