题目内容
6.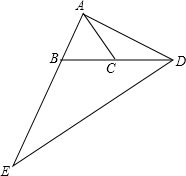 已知△ABC中,AB=AC,D为BC延长线上一点,且DC=BC,E是AB延长线上的一点,且BE=2AB,求证:DE=2AD.
已知△ABC中,AB=AC,D为BC延长线上一点,且DC=BC,E是AB延长线上的一点,且BE=2AB,求证:DE=2AD.
分析 由AB=AC,推出∠ABC=∠ACB,推出∠EBD=∠ACD,由BE=2AB=2AC,BD=2CD,推出$\frac{BE}{AC}$=$\frac{BD}{CD}$=2,推出△BED∽△CAD,即可解决问题.
解答 证明: ∵AB=AC,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠EBD=∠ACD,
∵BE=2AB=2AC,BD=2CD,
∴$\frac{BE}{AC}$=$\frac{BD}{CD}$=2,
∴△BED∽△CAD,
∴DE:AD=BE:AC=2,
∴ED=2AD.
点评 本题考查相似三角形的判定和性质、等腰三角形的性质等知识,解题的关键是熟练掌握相似三角形的判定和性质,属于中考常考题型.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
18.据电力部门统计,每天8:00-21:00是用电高峰期.简称“峰时”,21:00-次日8:00是用电低谷期,简称“谷时”.为了缓解供电需求紧张的矛盾,我市电力部门拟逐步统一换装“峰谷分时”电表,对用电实行“峰谷分时电价”新政策,具体见如表:
(1)小明家换表后第一个月用了“峰时”电和“谷时”电各50度,问小明家第一个月应交电费多少钱?
(2)小李家对换表后最初使用的95度电进行了测算,经测算比换表前使用95度电节约了5.9元,问小李家使用“峰时”电和“谷时”电分别是多少度?
| 时间 | 换表前 | 换表后 | |
| 峰时(8:00-21:00) | 谷时(21:00-8:00) | ||
| 电价 | 每度0.52元 | 每度0.55元 | 每度0.30元 |
(2)小李家对换表后最初使用的95度电进行了测算,经测算比换表前使用95度电节约了5.9元,问小李家使用“峰时”电和“谷时”电分别是多少度?
14.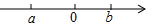 实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
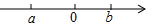 实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )
实数a,b在数轴上对应点得位置如图,则化简|a-b|-$\sqrt{{a}^{2}}$的结果是( )| A. | 2a-b | B. | b-2a | C. | b | D. | -b |
 ,其中
,其中 .
.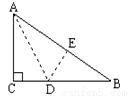

 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.