题目内容
11.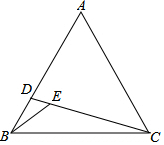 如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.
如图,在等边△ABC中,D为AB上一点,连接CD,在CD上取一点E,∠BEC=120°,连接BE.若CD=$\frac{14}{3}$,BE=2,△ACD的面积为$\frac{14}{3}$$\sqrt{3}$,则△BCE的面积为2$\sqrt{3}$.
分析 过B作BH⊥CD延长线于点H,根据三角函数可求BH=$\sqrt{3}$,HE=1,再根据三角形面积公式得到AB=2$\sqrt{7}$,BD=$\frac{1}{3}$×2$\sqrt{7}$,根据勾股定理和线段的和差故关系可得CE=4,再根据三角形面积公式即可求解.
解答 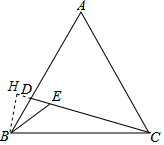 解:过B作BH⊥CD延长线于点H,
解:过B作BH⊥CD延长线于点H,
∵∠BEH=180°-120°=60°,BE=2,
∴BH=$\sqrt{3}$,HE=1,
S△BCD=$\frac{1}{2}$×$\sqrt{3}$×$\frac{14}{3}$=$\frac{7\sqrt{3}}{3}$,
∴S△BCA=$\frac{7\sqrt{3}}{3}$+$\frac{14\sqrt{3}}{3}$=7$\sqrt{3}$=$\frac{\sqrt{3}}{4}$AB2,
解得AB=2$\sqrt{7}$,
∴$\frac{{S}_{△BCD}}{{S}_{△BCA}}$=$\frac{2}{3}$=$\frac{AD}{AB}$,得BD=$\frac{1}{3}$×2$\sqrt{7}$,
在Rt△BDH中,DH=$\sqrt{B{D}^{2}-B{H}^{2}}$=$\frac{1}{3}$,DE=1-$\frac{1}{3}$=$\frac{2}{3}$,
CE=$\frac{14}{3}$-$\frac{2}{3}$=4,
∴S△BCE=$\frac{1}{2}$×$\sqrt{3}$×4=2$\sqrt{3}$.
故答案为:2$\sqrt{3}$.
点评 本题考查了勾股定理,等边三角形的性质,三角形面积,求得BH,CE的长是解题的关键.

练习册系列答案
相关题目
 的非负整数解是______.
的非负整数解是______.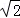 ,点A关于点B的对称点是点C,则点C所表示的数是( )
,点A关于点B的对称点是点C,则点C所表示的数是( )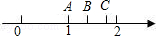
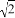 -1 B. 1+
-1 B. 1+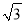 B.
B. 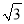 C. 2
C. 2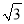 D. 3
D. 3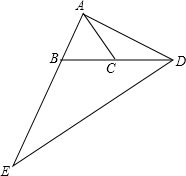 已知△ABC中,AB=AC,D为BC延长线上一点,且DC=BC,E是AB延长线上的一点,且BE=2AB,求证:DE=2AD.
已知△ABC中,AB=AC,D为BC延长线上一点,且DC=BC,E是AB延长线上的一点,且BE=2AB,求证:DE=2AD.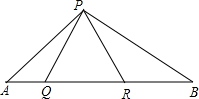 如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9.
如图,△PQR为等边三角形,∠APB=120°,若AQ=4,QR=6,则BR=9.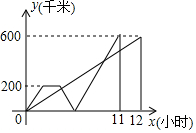 甲、乙两车在依次连通A、B、C三地的公路上行驶,甲车从B地出发匀速向C地行驶,同时乙车人B地出发匀速向A地行驶,到达A地并在A地停留1小时后,调头按原速向C地行驶.在两车行驶的过程中,甲、乙两车与B地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,当甲、乙两车相遇时,所用时间为10小时.
甲、乙两车在依次连通A、B、C三地的公路上行驶,甲车从B地出发匀速向C地行驶,同时乙车人B地出发匀速向A地行驶,到达A地并在A地停留1小时后,调头按原速向C地行驶.在两车行驶的过程中,甲、乙两车与B地的距离y(千米)与行驶时间x(小时)之间的函数图象如图所示,当甲、乙两车相遇时,所用时间为10小时.