题目内容
3.一直角三角形中一条直角边比另一条直角边大d厘米,斜边上高是h厘米,求斜边.分析 可设较小的直角边为x厘米,则较大的直角边为(x+d)厘米,根据勾股定理表示出斜边的长,再根据三角形面积公式列方程得到x的值,进一步得到斜边的长.
解答 解:设较小的直角边为x厘米,则较大的直角边为(x+d)厘米,
由勾股定理可得斜边L=$\sqrt{{x}^{2}+(x+d)^{2}}$厘米,
利用面积公式,可得$\frac{1}{2}$x(x+d)=$\frac{1}{2}$$\sqrt{{x}^{2}+(x+d)^{2}}$h,
所以x(x+d)=$\sqrt{{x}^{2}+(x+d)^{2}}$h=hL,
$\frac{{x}^{2}+(x+d)^{2}}{{x}^{2}(x+d)^{2}}$=$\frac{1}{{h}^{2}}$,
$\frac{1}{(x+d)^{2}}$+$\frac{1}{{x}^{2}}$=($\frac{1}{x}$-$\frac{1}{x+d}$)2+$\frac{2}{x(x+d)}$=$\frac{{d}^{2}}{[x(x+d)]^{2}}$+$\frac{2}{x(x+d)}$=$\frac{1}{{h}^{2}}$,
所以有$\frac{{d}^{2}}{(hL)^{2}}$+$\frac{2}{hL}$=$\frac{1}{{h}^{2}}$,
解得L=h±$\sqrt{{h}^{2}+{d}^{2}}$(负值舍去).
故斜边的长为h+$\sqrt{{h}^{2}+{d}^{2}}$.
点评 本题考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.同时考查了三角形面积的计算,利用三角形的面积公式得出x(x+d)=$\sqrt{{x}^{2}+(x+d)^{2}}$h=hL,然后根据分式混合运算的法则以及完全平方公式变形为$\frac{{d}^{2}}{(hL)^{2}}$+$\frac{2}{hL}$=$\frac{1}{{h}^{2}}$是解题的关键,本题的计算有一定的难度.

| A. | 射线OP上的点与OA,OB上任意一点的距离相等 | |
| B. | 射线OP上的点与边OA,OB的距离相等 | |
| C. | 射线OP上的点与OA各点的距离相等 | |
| D. | 射线OP上的点与OB上各的距离相等 |
| A. | 86.633×102 | B. | 8.6633×103 | C. | 0.86633×105 | D. | 8.6633×104 |
| A. | y1>y2 | B. | y1=y2 | C. | y1<y2 | D. | 不能比较 |
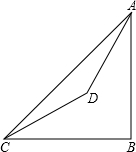 如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号).
如图,在山脚C测得山顶A的仰角为45°,沿着倾斜角为30°的斜坡前进300米到达D出,D处测得山顶的仰角为60°,求山高AB(结果保留根号). 如图,△ABC的三条高AD,BE,CF相交于点H,
如图,△ABC的三条高AD,BE,CF相交于点H,