题目内容
1．
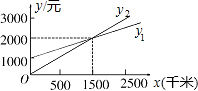某单位急需用车，但又不准备买车，他们准备和一个体车主或一国营出租车公司的一家签定月租车合同，设汽车每月行驶x千米，应付给个体车主的月费用是y1元，应付给出租车公司的月费是y2元，yl、y2分别与x之间的函数关系图象 （两条射线）如图所示，当每月行驶的路程等于1500时，租两家的费用相同？
分析 根据图象解答看两个函数的交点所对应的自变量的取值是多少即可．
解答 解：利用图象即可得出：当行驶路程为1500千米时，租用两家车的费用相同．
故答案为1500．
点评 此题主要考查了一次函数的应用，搞清楚交点意义是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
11．已知$\left\{\begin{array}{l}{x=2}\\{y=-2}\\{z=4}\end{array}\right.$是方程组$\left\{\begin{array}{l}{ax-\frac{1}{2}by+\frac{1}{4}cz=4}\\{\frac{1}{2}ax-by+\frac{1}{4}cz=2}\\{\frac{1}{2}ax-\frac{1}{2}by+\frac{1}{2}cz=6}\end{array}\right.$的解，则a，b，c的值（ ）
| A． | a=1，b=-1，c=3 | B． | a=-1，b=1，c=3 | C． | a=1，b=-1，c=-3 | D． | a=-1，b=1，c=-3 |
9．已知方程x2+nx-1=0的两实数根分别为α、β，则$\frac{β}{α}$+$\frac{α}{β}$的值为（ ）
| A． | n2+2 | B． | -n2+2 | C． | n2-2 | D． | -n2-2 |
16．若不等式组$\left\{\begin{array}{l}{a-x＞0}\\{x+1＞0}\end{array}\right.$无解，则a的取值范围是（ ）
| A． | a≥-1 | B． | a≤-1 | C． | a＞-1 | D． | a＜-1 |
某洗衣机洗涤衣服时，经历了进水，清洗，排水脱水四个连续的过程，其中进水，清洗，排水时洗衣机中的水量y（升）与时间x（分钟）之间的关系如图折线图所示，已知清洗时间为11分钟，排水时间为2分钟，则排水结束时洗衣机中剩下的水量为$\frac{82}{3}$升．
13．下列方程中：①x+y=x2；②$\frac{{x}^{3}}{x}$-x=0；③（x2-1）（x+1）=x（5+x）；④$\sqrt{5}$t2-6t=0；⑤y2=6；⑥$\frac{x}{3}$-1=$\frac{{x}^{2}}{4}$，属于一元二次方程的是（ ）
| A． | ①④⑤ | B． | ③④⑤ | C． | ④⑤⑥ | D． | ②⑤⑥ |
10．小明用17元买了1支笔和某种笔记本3个，已知笔记本的单价比笔的单价的2倍还多1元，设笔每支x元，笔记本每本y元，则所列方程组为（ ）
| A． | $\left\{\begin{array}{l}{x+3y=17}\\{x=2y+1}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{x+3y=17}\\{y=2x+1}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{y+3x=17}\\{x=2y+1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{y+3x=17}\\{y=2x+1}\end{array}\right.$ |
11．下列说法错误的是（ ）
| A． | 42的算术平方根为4 | B． | $\sqrt{4}$的算术平方根为$\sqrt{2}$ | ||
| C． | $\sqrt{{3}^{2}}$的算术平方根是$\sqrt{3}$ | D． | $\sqrt{81}$的算术平方根是9 |