题目内容
14．设a、b为两个不相等的实数，判断ab-a2与b2-ab大小．分析 利用作差法，把两个式子相减，进一步整理，利用完全平方公式因式分解，根据非负数的性质判定即可．
解答 解：∵ab-a2-（b2-ab）
=-（a2-2ab+b2）
=-（a-b）2
又a、b为两个不相等的实数，
∴-（a-b）2＜0，
∴ab-a2＜b2-ab．
点评 此题考查因式分解的实际运用，非负数的性质，比较两个整式的大小，作差法是常用的一种方法．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
4．当-2≤x≤1时，二次函数y=-（x-m）2+m2+1有最大值4，则实数m的值为（ ）
| A． | -$\sqrt{3}$或$\sqrt{3}$ | B． | -$\sqrt{3}$或2 | C． | -$\frac{7}{4}$或-$\sqrt{3}$或2 | D． | -$\frac{7}{4}$或-$\sqrt{3}$或$\sqrt{3}$或2 |
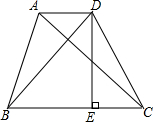如图，在等腰梯形ABCD中，AD∥BC，AB=CD，且AC⊥BD，DE是梯形的高，若S梯形ABCD=49cm2，求梯形的高．
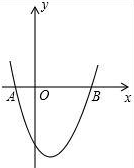如图，抛物线y=x2-x-2交x轴于A（-1，0），B两点，交y轴于C（0，-2），过A，C画直线．点M在抛物线上，以M为圆心的圆与直线AC相切，切点为H，若⊙M的半径为$\frac{4\sqrt{5}}{5}$，求点M的坐标．