题目内容
如图，∠ACB=90°，AC=2，BC=4，以点C为圆心，CA为半径的圆交AB于点D．求：（1）AD的长；
（2）△BCD的面积．
考点：垂径定理,勾股定理
专题：
分析：（1）首先过点C作CE⊥AD于点E，由∠ACB=90°，AC=2，BC=4，可求得AB的长，又由直角三角形斜边上的高等于两直角边乘积除以斜边，即可求得CE的长，由勾股定理求得AE的长，然后由垂径定理求得AD的长；
（2）由AB-AD，即可求得BD的长，继而求得答案．
（2）由AB-AD，即可求得BD的长，继而求得答案．
解答：
解：（1）过点C作CE⊥AD于点E，
则AE=DE，
∵∠ACB=90°，AC=2，BC=4，
∴AB=
=2
，
∴CE=
=
，
∴AE=
=
，
∴AD=2AE=
；
（2）∵AB=2
，AD=
，
∴BD=AB-AD=
，
∴S△BCD=
BD•CE=
×
×
=
．
解：（1）过点C作CE⊥AD于点E，则AE=DE，
∵∠ACB=90°，AC=2，BC=4，
∴AB=
| AC2+BC2 |
| 5 |
∴CE=
| AC•BC |
| AB |
4
| ||
| 5 |
∴AE=
| AC2-CE2 |
2
| ||
| 5 |
∴AD=2AE=
4
| ||
| 5 |
（2）∵AB=2
| 5 |
4
| ||
| 5 |
∴BD=AB-AD=
6
| ||
| 5 |
∴S△BCD=
| 1 |
| 2 |
| 1 |
| 2 |
4
| ||
| 5 |
6
| ||
| 5 |
| 12 |
| 5 |
点评：此题考查了垂径定理、勾股定理以及直角三角形的性质．此题难度适中，注意掌握辅助线的作法，注意掌握数形结合思想的应用．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
如图，点D是BC的中点，点E是AC的中点，点F是AB的中点．如果AB=BC=AC，那么与BD（BD除外）相等的线段共有（ ）| A、6条 | B、5条 | C、4条 | D、3条 |
如图，下列是一个几何体的三视图，请确定这个几何体的形状．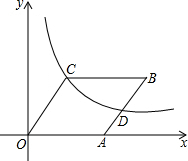
如图，?OABC的顶点B、C在第一象限，点A的坐标为（3，0），D为边AB的中点，反比例函数y=
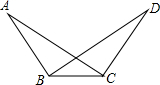如图，AC与BD相交于点O，且OB=OC，OA=OD．求证：∠ABC=∠DCB．