题目内容
在平面直角坐标系xOy中,直线y=-x+3与两坐标轴围成一个△AOB.现将背面完全相同,正面分别标有数1、2、3、3
、3
的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,再在剩下的4张卡片中任取一张,将该卡片上的数作为点P的纵坐标,请用所学的知识求出点P落在△AOB内部的概率.
| 3 |
| 3 |
考点:列表法与树状图法
专题:
分析:先列表求出点P的所有坐标,再找出落在△AOB内部的坐标个数,即可求出点P落在△AOB内部的概率.
解答:解:列表得:

因为直线y=-x+3与两坐标轴的交点坐标是(3,0)(0,3),
所以落在△AOB内部的点是(2,1)(1,2),
因为点P的坐标一共有20种情况,
所以点P落在△AOB内部的概率=
=
.

因为直线y=-x+3与两坐标轴的交点坐标是(3,0)(0,3),
所以落在△AOB内部的点是(2,1)(1,2),
因为点P的坐标一共有20种情况,
所以点P落在△AOB内部的概率=
| 2 |
| 20 |
| 1 |
| 10 |
点评:此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=
.
| m |
| n |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
某校初三•一班学生参加体育加试,第一小组引体向上的成绩如下表所示:
则这组学生引体向上个数的众数和中位数分别为( )
| 引体向上的个数 | 7 | 8 | 9 | 10 |
| 人数 | 2 | 1 | 4 | 5 |
| A、9.5和10 |
| B、9和10 |
| C、10和9.5 |
| D、10和9 |
若abc=1,且
+
+
=2003.则x等于( )
| x |
| 1+a+ab |
| x |
| 1+b+bc |
| x |
| 1+c+ac |
| A、1 | B、2003 |
| C、4006 | D、2008 |
已知两点A(1,2),B(3,1)到直线L的距离分别是
、
-
,则满足条件的直线L共有( )条.
| 2 |
| 5 |
| 2 |
| A、1 | B、2 | C、3 | D、4 |
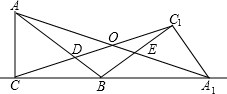 (S△AOD+S△A1BE)-(S△C1OE+S△CBD)=
(S△AOD+S△A1BE)-(S△C1OE+S△CBD)=