题目内容
4.已知数据x1、x2、x3的平均数为10,方差为2,求x12、x22、x32的平均数.分析 先由数据x1、x2、x3的平均数为10,得出x1+x2+x3=10×3=30,再根据方差为2,得到S2=$\frac{1}{3}$[(x1-10)2+(x2-10)2+(x3-10)2]=2,利用完全平方公式求出$\frac{1}{3}$(x12+x22+x32)=102,即x12、x22、x32的平均数是102.
解答 解:∵数据x1、x2、x3的平均数为10,
∴x1+x2+x3=10×3=30,
又∵方差为2,
∴S2=$\frac{1}{3}$[(x1-10)2+(x2-10)2+(x3-10)2]=$\frac{1}{3}$[x12+x22+x32-20(x1+x2+x3)+300]=$\frac{1}{3}$(x12+x22+x32-600+300)=$\frac{1}{3}$(x12+x22+x32)-100=2,
∴$\frac{1}{3}$[x12+x22+x32]=102,
即x12、x22、x32的平均数是102.
点评 本题考查了平均数与方差的意义.平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据中各数据与它们的平均数的差的平方的平均数,叫做这组数据的方差.计算公式是:s2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2].

练习册系列答案
相关题目
16.下列运算正确的是( )
| A. | (2a2)3=6a6 | B. | -a2b2•3ab3=-3a2b5 | ||
| C. | $\frac{b}{a-b}$+$\frac{a}{b-a}$=-1 | D. | $\frac{{a}^{2}-1}{a}$•$\frac{1}{a+1}$=-1 |
13. 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
 如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )
如图,正方形ABCD的边长为2,其面积标记为S1,以CD为斜边作等腰直角三角形,以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S2,…按照此规律继续下去,则S2015的值为( )| A. | ($\frac{\sqrt{2}}{2}$)2012 | B. | ($\frac{\sqrt{2}}{2}$)2013 | C. | ($\frac{1}{2}$)2012 | D. | ($\frac{1}{2}$)2013 |




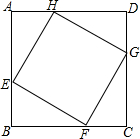 如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH.
如图,正方形ABCD的边长为8cm,E、F、G、H分别是AB、BC、CD、DA上的动点,且AE=BF=CG=DH. 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF.
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连接CD和EF.