题目内容
1.为了提倡低碳经济,某公司为了更好的节约能源,决定购买10台节省能源的新机器.现有甲、乙两种型号的设备,其中每台的价格、工作量如下表:| 节能设备 | 甲型 | 乙型 |
| 价格(万元/台) | 12 | b |
| 产量(吨/月 ) | 240 | 180 |
(1)求b的值;
(2)经预算,该公司购买节能设备的资金不超过110万元,请解答共有哪几种购买方案?
(3)在(2)的条件下,若每月要求产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
分析 (1)设购买了x台乙型设备,根据购买2台甲型设备比购买3台乙型设备少6万元,列出方程,求出x的值即可得出答案;
(2)设节省能源的新设备甲型设备x台,乙型设备(10-x)台,根据该公司购买节能设备的资金不超过110万元,列出不等式,求出x的值即可得出答案;
(3)因为公司要求每月的产量不低于2040吨,得出240x+180(10-x)≥2040,解之求出x的值,确定出方案,然后进行比较即可.
解答 解:(1)设购买了x台乙型设备,根据题意得:
24=3x-6,
解得:x=10,
则b的值是10;
(2)设购买节省能源的新设备甲型设备x台,乙型设备(10-x)台,
则:12x+10(10-x)≤110,
解得:x≤5,
∵x取非负整数∴x=0,1,2,3,4,5,
∴有6种购买方案.
(3)由题意:240x+180(10-x)≥2040,
∴x≥4,
∴x为4或5.
当x=4时,购买资金为:12×4+10×6=108(万元),
当x=5时,购买资金为:12×5+10×5=110(万元),
则最省钱的购买方案为,应选购甲型设备4台,乙型设备6台.
点评 本题考查一元一次不等式及二元一次方程组的应用,解决本题的关键是读懂题意,找到符合题意的不等关系式及所求量的等量关系.要会用分类的思想来讨论求得方案的问题.

练习册系列答案
相关题目
9.绵阳到某地相距n千米,提速前火车从绵阳到某地要t小时,提速后行车时间减少了0.5小时,提速后火车的速度比原来速度快了( )
| A. | $\frac{n}{t-0.5}$ | B. | $\frac{n}{t}$ | C. | $\frac{n}{t-0.5}$-$\frac{n}{t}$ | D. | $\frac{n}{t}$-$\frac{n}{t-0.5}$ |
16.当x取任意实数时,下列各根式有意义的是( )
| A. | $\sqrt{x+1}$ | B. | $\sqrt{\frac{x-1}{2}}$ | C. | $\sqrt{\frac{3}{{x}^{2}}}$ | D. | $\sqrt{|x|+1}$ |
13.以下列各组线段为边,能组成三角形的是( )
| A. | 2cm、2cm、4cm | B. | 8cm、6cm、3cm | C. | 2cm、6cm、3cm | D. | 11cm、4cm、6cm |
11.已知|3a-2b-12|+(a+2b+4)2=0.则( )
| A. | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{a=2}\\{b=-3}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{a=-3}\\{b=2}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{a=-2}\\{b=-3}\end{array}\right.$ |
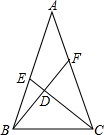 如图,在△ABC中,AB=AC,点E、F分别在AB和AC上,CE与BF相交于点D.若AE=CF,D为BF的中点,则$\frac{AE}{AB}$的值为$\frac{\sqrt{5}-1}{2}$.
如图,在△ABC中,AB=AC,点E、F分别在AB和AC上,CE与BF相交于点D.若AE=CF,D为BF的中点,则$\frac{AE}{AB}$的值为$\frac{\sqrt{5}-1}{2}$.
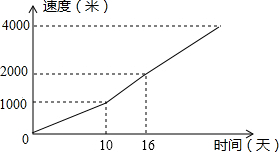 为了改善锦州市民的休闲、娱乐环境,从2013年起政府启动了小凌河水生态环境综合治理工程,有一段长为4000米的河堤需要治理,甲工程单独做了10天后,为了加快速度,决定由甲、乙两个工程队合做完成剩下的全部工程,已知工程队完成该河段河堤治理工程的进度(米)与时间(天)之间的关系如图所示:
为了改善锦州市民的休闲、娱乐环境,从2013年起政府启动了小凌河水生态环境综合治理工程,有一段长为4000米的河堤需要治理,甲工程单独做了10天后,为了加快速度,决定由甲、乙两个工程队合做完成剩下的全部工程,已知工程队完成该河段河堤治理工程的进度(米)与时间(天)之间的关系如图所示: