题目内容
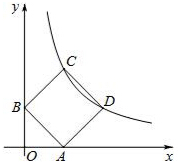 如图,矩形ABCD的顶点C、D在反比例函数y=
如图,矩形ABCD的顶点C、D在反比例函数y=| k |
| x |
| 5 |
考点:相似三角形的判定与性质,反比例函数图象上点的坐标特征,全等三角形的判定与性质
专题:
分析:作CE⊥y轴于点E,DF⊥x轴于点F,根据四边形ABCD是矩形得出BC=AD,根据相似三角形的判定定理得出△OAB∽△EBC∽△FDA,故∠EBC=∠FDA,∠BCE=∠DAF,在△EBC与△FAD中,由ASA定理得出△OAB≌△FAD,设OB=y,则OA=x,根据AB=2AD可得AF=
y,BE=
x,再由勾股定理得出关于xy的方程组,求出x,y的值即可.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
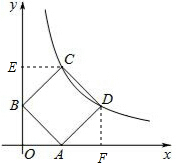 解:作CE⊥y轴于点E,DF⊥x轴于点F,
解:作CE⊥y轴于点E,DF⊥x轴于点F,
∵四边形ABCD是矩形,
∴BC=AD,
∵∠ABO+∠OAB=90°,∠ABO+∠CBE=90°,
∴∠OAB=∠CBE,
∵∠AEB=∠AOB=90°,
∴△OAB∽△EBC.
同理可得,△OAB∽△FDA,
∴△OAB∽△EBC∽△FDA,
∴∠EBC=∠FDA,∠BCE=∠DAF,
在△EBC与△FAD中,
,
∴△OAB≌△FAD(ASA),
设OB=y,则OA=x,
∵AB=2AD,
∴AF=
y,BE=
x,
∴
,
解得x=y=
,
∴k=(
x+y)•
y=
.
 解:作CE⊥y轴于点E,DF⊥x轴于点F,
解:作CE⊥y轴于点E,DF⊥x轴于点F,∵四边形ABCD是矩形,
∴BC=AD,
∵∠ABO+∠OAB=90°,∠ABO+∠CBE=90°,
∴∠OAB=∠CBE,
∵∠AEB=∠AOB=90°,
∴△OAB∽△EBC.
同理可得,△OAB∽△FDA,
∴△OAB∽△EBC∽△FDA,
∴∠EBC=∠FDA,∠BCE=∠DAF,
在△EBC与△FAD中,
|
∴△OAB≌△FAD(ASA),
设OB=y,则OA=x,
∵AB=2AD,
∴AF=
| 1 |
| 2 |
| 1 |
| 2 |
∴
|
解得x=y=
| 10 |
∴k=(
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
点评:本题考查的是相似三角形的判定与性质,根据题意作出相似三角形,再由反比例函数的性质及勾股定理求解是解答此题的关键.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
两圆的半径分别为3cm和4cm,且两圆的圆心距为7cm,则这两圆的公切线条数共有( )
| A、1条 | B、2条 | C、3条 | D、4条 |
 已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上.
已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上. 从A地到C地,可供选择的方案有走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有( )
从A地到C地,可供选择的方案有走水路、走陆路、走空中.从A地到B地有2条水路、2条陆路,从B地到C地有3条陆路可供选择,走空中从A地不经B地直接到C地.则从A地到C地可供选择的方案有( )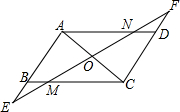 如图,已知:AB=DC,AD=BC.
如图,已知:AB=DC,AD=BC.