题目内容
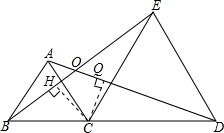
 已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上.
已知,△ABC和△ECD都是等边三角形,且点B、C、D在一条直线上.(1)求证:BE=AD;
(2)若AD,BE交于O点,连接OC,求证:OC平分∠BOD.
考点:全等三角形的判定与性质,等边三角形的性质
专题:证明题
分析:(1)利用等边三角形的性质和已知条件证明△ACD≌△BCE即可,
(2)作CH⊥BE于H,CQ⊥AD于Q,如图,由△ACD≌△BCE得到CQ=CH,于是根据角平分线的判定定理即可得到CO平分∠BOD.
(2)作CH⊥BE于H,CQ⊥AD于Q,如图,由△ACD≌△BCE得到CQ=CH,于是根据角平分线的判定定理即可得到CO平分∠BOD.
解答:
证明:(1)∵△ABC和△ECD都是等边三角形,
∴AC=BC,EC=DC,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
 即∠ACD=∠BCE,
即∠ACD=∠BCE,
∴△ACD≌△BCE,
∴AD=BE;
(2)作CH⊥BE于H,CQ⊥AD于Q,如图,
∵△ACD≌△BCE,
∴CQ=CH,
∴CO平分∠BOD.
∴AC=BC,EC=DC,∠ACB=∠ECD=60°,
∴∠ACB+∠ACE=∠ECD+∠ACE,
 即∠ACD=∠BCE,
即∠ACD=∠BCE,∴△ACD≌△BCE,
∴AD=BE;
(2)作CH⊥BE于H,CQ⊥AD于Q,如图,
∵△ACD≌△BCE,
∴CQ=CH,
∴CO平分∠BOD.
点评:本题考查了全等三角形的判定与性质:判定三角形全等的方法有“SSS”、“SAS”、“ASA”、“AAS”;全等三角形的对应边相等.也考查了等边三角形的判定与性质.

练习册系列答案
相关题目
已知圆锥的母线为6,底面圆的半径为4,则此圆锥的侧面积是( )
| A、12π | B、15π |
| C、24π | D、30π |
关于x的方程x2+2kx+k-1=0的根的情况描述正确的是( )
| A、k为任何实数,方程都没有实数根 |
| B、k为任何实数,方程都有两个不相等的实数根 |
| C、k为任何实数,方程都有两个相等的实数根 |
| D、根据k的取值不同,方程根的情况分为没有实数根、有两个不相等的实数根和有两个相等的实数根三种 |
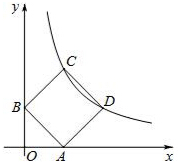 如图,矩形ABCD的顶点C、D在反比例函数y=
如图,矩形ABCD的顶点C、D在反比例函数y=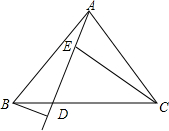 如图所示,△ABC中,AB=AC,∠BAC=80°,过点A作射线AD,点E在AD上,∠ADB=100°.∠CED=80°,
如图所示,△ABC中,AB=AC,∠BAC=80°,过点A作射线AD,点E在AD上,∠ADB=100°.∠CED=80°,