题目内容
已知在△ABC中,AB=AC=10,AD为BC边上的高,若△ABC的面积为48,则点D到AB的距离为 .
考点:勾股定理,等腰三角形的性质
专题:
分析:首先利用等腰三角形的性质,证明BD=CD,进而证明△ABD的面积为△ABC的面积的一半,结合面积公式即可解决问题.
解答:解:∵AB=AC,AD⊥BC,
∴BD=CD;
故S△ABD=S△ACD=
S△ABC;
设点D到AB的距离为h,
则S△ABD=
AB•h;
又∵AB=10,S△ABC=48,
∴5h=24,
∴h=
,
即点D到AB的距离为
.
∴BD=CD;
故S△ABD=S△ACD=
| 1 |
| 2 |
设点D到AB的距离为h,
则S△ABD=
| 1 |
| 2 |
又∵AB=10,S△ABC=48,
∴5h=24,
∴h=
| 24 |
| 5 |
即点D到AB的距离为
| 24 |
| 5 |
点评:该命题主要考查了等腰三角形的性质及其应用问题;解题的关键是灵活运用有关知识来判断、分析、证明或求解.

练习册系列答案
相关题目
在下面各数中无理数的个数有( )
|-
|,-3.14,
,0.1010010001…,+1.99,-
.
|-
| 3 |
| 4 |
| 22 |
| 7 |
| π |
| 3 |
| A、5个 | B、4个 | C、3个 | D、2个 |
如果一个正多边形绕它的中心旋转90°就和原来的图形重合,那么这个正多边形是( )
| A、正三角形 | B、正方形 |
| C、正五边形 | D、正六边形 |
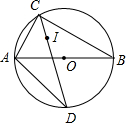 如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD.
如图,AB是⊙O的直径,点C是⊙O上一点,点I是△ABC(AC<AB)的内心,CI的延长线交⊙O于点D,连AD. 如图,在△ABC中,AB=8,AC=6,BC=10.线段BC所在直线以每秒2个单位的速度沿与其垂直的方向上平行移动,记x秒时,该直线在△ABC内的部分的长度为y.试写出y关于x的函数关系式,并在平面直角坐标系中画出这一函数的图象.
如图,在△ABC中,AB=8,AC=6,BC=10.线段BC所在直线以每秒2个单位的速度沿与其垂直的方向上平行移动,记x秒时,该直线在△ABC内的部分的长度为y.试写出y关于x的函数关系式,并在平面直角坐标系中画出这一函数的图象.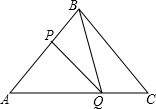 如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发沿AB方向以4cm/s的速度向B点运动,同时点Q从C点出发沿CA方向以3cm/s的速度向A点运动,设运动时间为x s.
如图所示,在△ABC中,BA=BC=20cm,AC=30cm,点P从A点出发沿AB方向以4cm/s的速度向B点运动,同时点Q从C点出发沿CA方向以3cm/s的速度向A点运动,设运动时间为x s.
 如图,△ABC与△DEF关于直线l成轴对称,
如图,△ABC与△DEF关于直线l成轴对称,