题目内容
5．先化简，再求值：（$\frac{2x-1}{x+1}$-x+1）÷$\frac{x-2}{{x}^{2}+2x+1}$，其中x=$\sqrt{2}$+1．分析 原式括号中两边通分并利用同分母分式的减法法则计算，同时利用除法法则变形，约分得到最简结果，把x的值代入计算即可求出值．
解答 解：（$\frac{2x-1}{x+1}$-x+1）÷$\frac{x-2}{{x}^{2}+2x+1}$，
=$\frac{2x-1-{x}^{2}-x+x+1}{x+1}×\frac{{x}^{2}+2x+1}{x-2}$
=-x（x+1）
=-x2-x，
把x=$\sqrt{2}$+1代入$-{x}^{2}-x=-（\sqrt{2}+1）^{2}-（\sqrt{2}+1）=-4-3\sqrt{2}$．
点评 此题考查了分式的化简求值，熟练掌握运算法则是解本题的关键．
练习册系列答案
相关题目
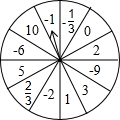小亮自己设计了一个如图所示的自由转动的均匀的转盘，转盘被等分成12个扇形，每一个扇形里写有一个有理数，自由转动转盘，转盘停止后，分别求下列事件发生的概率：
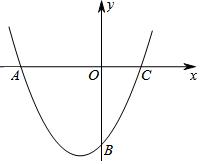已知抛物线经过A（-4，0），B（0，-4），C（2，0）三点．
如图，△ABC中，∠ACB=90°，∠1=∠A．