题目内容
当x= 时,多项式3-2x2+4x取得最 值.
考点:配方法的应用,非负数的性质:偶次方
专题:
分析:先用配方法把多项式化为完全平方与一个数的和的形式,再根据非负数的性质进行解答.
解答:解:3-2x2+4x
=-2(x2-2x)+3
=-2(x-1)2+1.
∵(x-1)2≥0,
∴-2(x-1)2+1≤1,
∴当x=1时,多项式3-2x2+4x取得最 大值1.
故答案是:1;大.
=-2(x2-2x)+3
=-2(x-1)2+1.
∵(x-1)2≥0,
∴-2(x-1)2+1≤1,
∴当x=1时,多项式3-2x2+4x取得最 大值1.
故答案是:1;大.
点评:此题考查了学生的应用能力,解题时要注意配方法的步骤.注意在变形的过程中不要改变式子的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
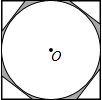 已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )
已知正方形的内切圆O半径为2,如图,正方形的四个角上分别有一个直角三角形,如果直角三角形的第三边与圆O相切且平行于对角线.则阴影部分的面积为( )A、32
| ||
B、
| ||
| C、1 | ||
| D、16-4π |
下列计算正确的是( )
| A、6x+4x=10+x |
| B、4x-3x=1 |
| C、8a-2b=6ab |
| D、3ab-3ba=0 |
下列各数中,最小的数是( )
| A、-2 | B、1 | C、0 | D、-3 |
 如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5).
如图,在△ABC中,AB=AC=10cm,BD⊥AC于点D,BD=8cm.点M从点A出发,沿AC的方向匀速运动,速度为2cm/s;同时直线PQ由点B出发,沿BA的方向匀速运动,速度为1cm/s,运动过程中始终保持PQ∥AC,直线PQ交AB于点P、交BC于点Q、交BD于点F.连接PM,设运动时间为t秒(0<t<5). 如图,GC交AB于点M,GH分别交AB,EF于点N,HD平分∠GHF,∠1+∠C=180°,∠2=∠3=60°,求证:CD∥EF.
如图,GC交AB于点M,GH分别交AB,EF于点N,HD平分∠GHF,∠1+∠C=180°,∠2=∠3=60°,求证:CD∥EF. 上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米.
上海世博会中国馆共分为国家馆和地区馆两部分,国家馆居中升起、层叠出挑,采用极富中国建筑文化元素的红色“斗冠”造型,由地下一层、地上六层组成.小明通过上网查阅资料得知,国家馆地上六层均为正方形,如图所示,最上面一层正方形边长为a米,以下每层的边长比上一层减少b米. 如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )
如图,以O为圆心,任意长为半径画弧,与射线OM相交于点A,再以点A为圆心,AO长为半径画弧,两弧交于点B,画射线OB,则sin∠AOB的值等于( )