题目内容
19.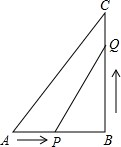 已知,如图在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发沿AB方向向终点点B匀速移动,速度为1cm/s,点Q由点B出发沿BC方向向终点点C匀速移动,速度为2cm/s.如果动点P,Q同时从A,B出发,当P或Q到达终点时运动停止.几秒后,以Q,B,P为顶点的三角形与△ABC相似?
已知,如图在Rt△ABC中,∠B=90°,AB=6cm,BC=8cm,点P由点A出发沿AB方向向终点点B匀速移动,速度为1cm/s,点Q由点B出发沿BC方向向终点点C匀速移动,速度为2cm/s.如果动点P,Q同时从A,B出发,当P或Q到达终点时运动停止.几秒后,以Q,B,P为顶点的三角形与△ABC相似?
分析 设t秒后,以Q,B,P为顶点的三角形与△ABC相似;则PB=(6-t)cm,BQ=2tcm,分两种情况:①当$\frac{PB}{AB}=\frac{BQ}{BC}$时;②当$\frac{PB}{BC}=\frac{BQ}{AB}$时;分别解方程即可得出结果.
解答 解:设t秒后,以Q,B,P为顶点的三角形与△ABC相似;
则PB=(6-t)cm,BQ=2tcm,
∵∠B=90°,
∴分两种情况:
①当$\frac{PB}{AB}=\frac{BQ}{BC}$时,
即$\frac{6-t}{6}=\frac{2t}{8}$,
解得:t=2.4;
②当$\frac{PB}{BC}=\frac{BQ}{AB}$时,
即$\frac{6-t}{8}=\frac{2t}{6}$,
解得:t=$\frac{18}{11}$;
综上所述:2.4秒或$\frac{18}{11}$秒时,以Q,B,P为顶点的三角形与△ABC相似.
点评 本题考查了相似三角形的判定方法、解方程;熟练掌握相似三角形的判定方法,分两种情况进行讨论是解决问题的关键.

练习册系列答案
相关题目
7.下面两个三角形一定相似的是( )
| A. | 两个等边三角形 | B. | 两个等腰三角形 | C. | 两个直角三角形 | D. | 两个锐角三角形 |
4.“十一”黄金周期间,某市风景区在7天假期中每天旅游的人数变化如下表(正数表示比前一天多的人数,负数表示比前一天少的人数):
已知9月30日的游客人数为2万人,请回答下列问题:
(1)七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
(2)求这7天的游客总人数是多少万人.
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化(单位:万人) | 1.6 | 0.8 | 0.4 | -0.4 | -0.8 | 0.2 | -1.2 |
(1)七天内游客人数最多的是哪天,最少的是哪天?它们相差多少万人?
(2)求这7天的游客总人数是多少万人.
 如图,△ABC的内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,以下结论:
如图,△ABC的内角∠ABC和外角∠ACD的平分线交于点E,BE交AC于点F,过点E作EG∥BD交AB于点G,交AC于点H,连接AE,以下结论: